The Spline Animator defines an animation using the keyframe paradigm. The basic objective is to define each frame of the animation in terms of a relatively small set of keyframes which indicate the position of the camera at critical portions of the animation. Each keyframe includes a keytime which orders the set of keyframes. An animation frame at a particular time t is then defined as some combination of the keyframe before time t and the keyframe after time t. For the Spline Animator, this combination is created by fitting a cubic spline through the camera parameters of each keyframe and evaluating the resulting spline for animation frames falling between keyframes.
There are three concepts the user should be familiar with in order to use the Spline Animator to do keyframe animation:
The Spline Animator records camera position, look-at location, view up, and current keytime information each instant a keyframe is set. When at least two keyframes have been created, the Spline Animator creates splines for each of the above components using keytime for parameterization of the splines. In AVS, camera position, look-at location, and view up are each 3-tuples of the form (x,y,z). Thus a total of nine splines are necessary, three for each component, to completely interpolate a set of keyframes.
Once the splines have been generated, framerate information
is then used to determine how we should evaluate the splines. Keytime
is always considered to be expressed in seconds and framerate is
considered to be expressed in frames/second. Furthermore, framerate
must always be an integer. It will be necessary to evaluate our splines
each time a new frame is produced. Thus if our framerate is 
frames/second
and the total length of our animation is 
seconds is will be necessary to
evaluate the splines 
times. Since we require frames to
be equally spaced in time, we will evaluate our splines every 
seconds.
The evaluation process for n splines can be expressed by the simple loop:
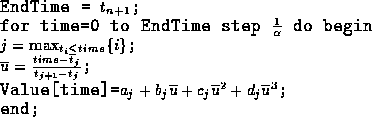
where Value is a special array which we allow to be indexed by real numbers, and which we use to store the results of the spline evaluation. In practice, we do not actually need to find the appropriate spline every time through the loop. However, we do so here for clarity. Also, recall that we have nine splines thus the loop above will need to be executed nine times. Fortunately, with the obvious optimizations, the loop above executes quite rapidly.