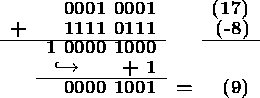As in sign-magnitude, the leftmost bit indicates the sign of an integer in complement representation. The representation for positive integers is the same as unsigned with the leftmost bit = 0.
Negative integers are formed by reversing all bits to form the bitwise complement of a positive integer. If I is the (n+1) bit binary sequence:
![]()
then -I in one's complement is given by:
![]()
where ![]() for all i.
for all i.
Let I be a negative one's complement integer. The value of I is obtained by forming its one's complement:
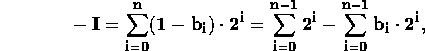
since ![]() . Thus,
. Thus,
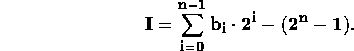
Negative one's complement integers are formed by subtracting a bias of
![]() from the positive integers. Taking into account the sign
bit
from the positive integers. Taking into account the sign
bit ![]() , the value for a positive or
negative (n+1) bit one's complement integer is:
, the value for a positive or
negative (n+1) bit one's complement integer is:
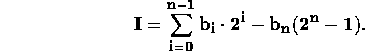
The range of values for an (n+1) bit one's complement integer is
![]() to
to ![]() .
.
Since the complement of 0 is ![]() , there are
different representations for +0 and -0 in one's complement.
, there are
different representations for +0 and -0 in one's complement.
Examples of 8-bit one's complement numbers:

The range of 8-bit one's complement integers is -127 to +127.
Addition of signed numbers in one's complement is performed using binary addition with end-around carry. If there is a carry out of the most significant bit of the sum, this bit must be added to the least significant bit of the sum.
To add decimal 17 to decimal -8 in 8-bit one's complement: