Secure Hash Algorithm SHA-256
CS
463/480 Lecture, Dr.
Lawlor
A "hash algorithm" converts a variable-length message into a
fixed-size digest.
d = H(m);
Hashes are used extensively in modern crypto--for example, passwords
are protected by sending only the hash across the network, not the
actual password. HTTPS certificates are just a signed
hash. For BitCoin, the links holding together the block chain
(the electronic ledger) are hashes.
We want two contradictory properties from a good hash algorithm:
- Preimage resistance: given a digest d, it's hard
to find the message m. This is the "trapdoor" or "one-way"
nature of a hash, as used to protect things like passwords--an
attacker might know the hash, but still can't figure out the
password. It's always possible to brute force check the
hashes of all possible passwords, but this takes exponential
time. Most known hashes are still secure against preimage
attacks.
- Collision resistance: it's hard to find two messages m1
and m2 such that H(m1)=H(m2). This is key to things like
digital signatures, where you might get "Dr. Lawlor runs
lawlor.cs.uaf.edu" signed, but want to secretly substitute a
message like "Dr. Lawlor runs whitehouse.gov". The Birthday
attack means you can always find collisions in an n-bit
hash using about 2n/2 storage. Some hashes like
MD5 are broken much worse than this against collisions, so
people can generate
hash collisions, for example by adding binary comments in
the postscript file. There are worries
about SHA-1 collision resistance, with known attacks
nearly feasible: although nobody's actually published any
collisions yet, it's considered a matter of time (browsers are finally
phasing out SHA-1 certificate support).
It's easy to come up with trivial hash algorithms that have one of
these properties but not the other. For example, the null hash
H(m)=0 has perfect preimage resistance, but no collision resistance
(all messages have the same hash!). Conversely, the "message
hash" H(m)=m has perfect collision resistance, but no preimage
resistance (the hash *is* the message).
The pigeonhole principle means hash collisions are inevitable:
SHA-256 takes an input of arbitrary length, and generates an output
of 256 bits, so many inputs clearly must have the same output.
You can turn any ordinary symmetric encryption algorithm
C(plaintext,key) into a slow but decent hash algorithm, by
encrypting a fixed plaintext (for example, all zeros) and using the
message as the key. (Thought problem: why not avoid this by
using the message as plaintext, and all zeros as the key?) The
only problem is most symmetric algorithms use a fixed-size key, so
you need to make multiple passes to consume the whole key.
Microsoft famously misused this technique for LM hash passwords:
they based the hash on DES, which could only fit 7 bytes of the
password at a time; for longer passwords instead of chaining they
simply output a separate hash for each 7 bytes of the password,
which breaks a nice long secure password into independent chunks
that can be brute forced one by one!
SHA-256
The core of SHA-256 is a round-based bit
mixing function applied to a 256-bit block of data.
Each round consists of bit mixing
between eight integers or "state variables", here named a-h.
// SHA-256 round function:
... load Wi from the
data, or mixed from data in later rounds ...
// Mixing
h +=
(ror(e,6)^ror(e,11)^ror(e,25)) + (g^(e&(f^g))) + K[i] + Wi; //
"Ch"
d += h;
h +=
(ror(a,2)^ror(a,13)^ror(a,22)) + ((a&b)|(c&(a|b))); //
"Maj"
// Cyclic shift of
variables:
UInt32 old_h=h;
h=g; g=f; f=e; e=d;
d=c; c=b; b=a; a=old_h;
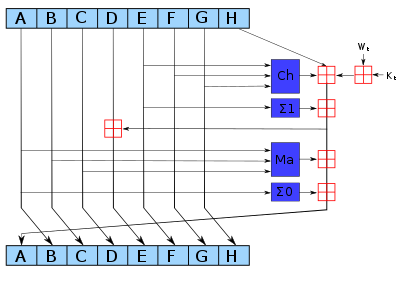
This is repeated for 64 rounds per block
of the message. The value of the output hash is just the sum
of the ending values of the a-h variables after running each
block.
Here's the full code. Note we
might need to buffer up message data until we accumulate each full
block to hash, and the special work at the end of the message (add
a one bit, pad with zeros to the end of the block, and add message
length in bits). This takes about 600 nanoseconds per block,
or a little under 2 million short hashes per second (per core of a
Sandy Bridge machine).
/*
Single-file SHA-256 hash in C++
2013-02-19 : Orion Lawlor : Public domain
2010-06-11 : Igor Pavlov : Public domain
http://cpansearch.perl.org/src/BJOERN/Compress-Deflate7-1.0/7zip/C/Sha256.c
This code is based on public domain code from Wei Dai's Crypto++ library.
*/
#include <string.h> /* for size_t and memset (to zero) */
#include <string> /* for std::string */
/*
This class computes SHA256 message digests.
*/
class SHA256 {
public:
/* This type needs to be at least 32 bits, unsigned */
typedef unsigned int UInt32;
/* This is the type of the data you're processing */
typedef unsigned char Byte;
/* This is the data type of a message digest, the hash output. */
class digest {
public:
enum {size=32}; // bytes in a message digest
SHA256::Byte data[size]; // binary digest data
// Equality. This is useful for "if (cur==target)" tests.
bool operator==(const digest &other) const {
for (int i=0;i<size;i++)
if (data[i]!=other.data[i])
return false;
return true;
}
// Less-than. This is mostly useful for std::map<SHA256::digest, ...>
bool operator<(const digest &other) const {
for (int i=0;i<size;i++)
if (data[i]<other.data[i])
return true;
else if (data[i]>other.data[i])
return false;
return false;
}
// Convert digest to an ASCII string of hex digits (for printouts)
std::string toHex() const;
};
/* External Interface */
SHA256(); // constructor. Sets up initial state.
// Add raw binary message data to our hash.
// You can call this repeatedly to add as much data as you want.
void add(const void *data, size_t size);
// Finish this message and extract the digest.
// Resets so you can add the next message, if desired.
SHA256::digest finish(void);
~SHA256(); // destructor. Clears out state and buffered data.
/* private: Internal Interface (left public, for debug's sake) */
// This is the internal state of the hash.
UInt32 state[8];
// This is how many message bytes we've seen so far.
size_t count;
// This buffers up to a whole block of data
Byte buffer[64];
// Reset to initial values.
void init();
// Process the finished block of data in "buffer"
void block();
public:
/* This is the *really* easy version: given a string as input, return the digest as output.
std::cout<<"SHA-256: "<<SHA256::digestString(someString).toHex()<<"\n";
*/
static inline SHA256::digest digestString(const std::string &src) {
SHA256 hash;
hash.add(&src[0],src.length());
return hash.finish();
}
};
/*
Implementation: SHA-256 Hash in C++
*/
/************** Bit twiddling and round operations for SHA256 *************/
/* Define bit rotate operations. These work like:
UInt32 ror(UInt32 value,UInt32 bitcount)
*/
#ifdef _MSC_VER /* Windows bit rotate from standard library */
# include <stdlib.h>
# define rol(x, n) _rotl((x), (n))
# define ror(x, n) _rotr((x), (n))
#else /* portable (Linux, Mac, etc) bit rotate */
# define rol(x, n) (((x) << (n)) | ((x) >> (32 - (n))))
# define ror(x, n) (((x) >> (n)) | ((x) << (32 - (n))))
#endif
/* These are the round keys, one per round.
These are the first 32 bits of the fractional parts
of the cube roots of the first 64 primes 2..311.
*/
static const SHA256::UInt32 K[64] = {
0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5,
0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3,
0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc,
0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7,
0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13,
0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3,
0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5,
0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208,
0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2
};
/* This sets up the Sha256 initial state, at the start of a message. */
void SHA256::init()
{
/* These are the first 32 bits of the fractional parts
of the square roots of the first 8 primes 2..19. */
state[0] = 0x6a09e667;
state[1] = 0xbb67ae85;
state[2] = 0x3c6ef372;
state[3] = 0xa54ff53a;
state[4] = 0x510e527f;
state[5] = 0x9b05688c;
state[6] = 0x1f83d9ab;
state[7] = 0x5be0cd19;
count = 0;
}
SHA256::SHA256() {
init();
}
/* This adds another block of data to our current state.
This is our main transforming/mixing function. */
void SHA256::block()
{
unsigned i;
enum {ROUND_COUNT=64};
UInt32 KWi[ROUND_COUNT]; // Per-round key + work data
// First part of W is just the incoming message data */
#define s0(x) (ror(x, 7) ^ ror(x,18) ^ (x >> 3))
#define s1(x) (ror(x,17) ^ ror(x,19) ^ (x >> 10))
UInt32 W[16]; // Work buffer: 0-15 are straight from the data
for (i = 0; i < 16; i++) {
W[i]=
((UInt32)(buffer[i * 4 ]) << 24) +
((UInt32)(buffer[i * 4 + 1]) << 16) +
((UInt32)(buffer[i * 4 + 2]) << 8) +
((UInt32)(buffer[i * 4 + 3])); // big-endian 32-bit load
KWi[i]=W[i]+K[i];
}
// The rest of W is a scrambled copy of the original data
for (;i<ROUND_COUNT;i++)
{
W[i&15] += s1(W[(i-2)&15]) + W[(i-7)&15] + s0(W[(i-15)&15]);
KWi[i] = W[i&15]+K[i];
}
UInt32 a,b,c,d,e,f,g,h; /* local copies of state, for performance */
a=state[0]; b=state[1]; c=state[2]; d=state[3];
e=state[4]; f=state[5]; g=state[6]; h=state[7];
// This is the main data transform loop
for (i = 0; i < ROUND_COUNT; i++) {
// SHA-256 round function:
// Mixing
h += (ror(e,6)^ror(e,11)^ror(e,25)) + (g^(e&(f^g))) + KWi[i]; // "Ch"
d += h;
h += (ror(a,2)^ror(a,13)^ror(a,22)) + ((a&b)|(c&(a|b))); // "Maj"
// Cyclic shift of variables:
UInt32 old_h=h;
h=g; g=f; f=e; e=d; d=c; c=b; b=a; a=old_h;
}
// Add result back into state array
state[0]+=a; state[1]+=b; state[2]+=c; state[3]+=d;
state[4]+=e; state[5]+=f; state[6]+=g; state[7]+=h;
/* Wipe temporary variables, so they're not left in memory on the stack */
memset(W, 0, sizeof(W));
memset(KWi, 0, sizeof(KWi));
}
// Add raw binary message data to our hash.
void SHA256::add(const void *data, size_t size)
{
const Byte *dataptr=(const Byte *)data;
UInt32 curBufferPos = (UInt32)count & 0x3F; /* location within last block */
while (size > 0)
{
buffer[curBufferPos++] = *dataptr++; // copy next byte of data
count++; // message got longer
size--; // user data got shorter
if (curBufferPos >= 64) // we have one whole block finished
{
curBufferPos = 0;
block();
}
}
}
/* End Sha256 processing, and write out message digest. */
SHA256::digest SHA256::finish(void)
{
size_t lenInBits = count*8; // i.e., times 8 bits per byte
UInt32 curBufferPos = (UInt32)count & 0x3F; // 0x3f is mask to wrap around to buffer size
unsigned i;
buffer[curBufferPos++] = 0x80; // standard specifies "add a one bit...
while (curBufferPos != (64 - 8)) // ...then pad with zeros to end of block"
{
curBufferPos &= 0x3F;
if (curBufferPos == 0)
block();
buffer[curBufferPos++] = 0; // zero out rest of block
}
// Finally, add message length, in bits, as big-endian 64 bit number
for (i = 0; i < 8; i++)
{
buffer[curBufferPos++] = (Byte)(lenInBits >> 56);
lenInBits <<= 8;
}
block(); // transform last block (including length)
// Copy state out as big-endian integers.
SHA256::digest output;
for (i = 0; i < 8; i++)
{
output.data[i*4+0] = (Byte)(state[i] >> 24);
output.data[i*4+1] = (Byte)(state[i] >> 16);
output.data[i*4+2] = (Byte)(state[i] >> 8);
output.data[i*4+3] = (Byte)(state[i]);
}
init(); // reset for next trip around
return output;
}
SHA256::~SHA256()
{
// To keep from leaving any sensitive data in memory, zero out our buffers.
memset(state,0,sizeof(state));
count=0;
memset(buffer,0,sizeof(buffer));
}
std::string SHA256::digest::toHex() const
{
std::string ret="";
for (int i=0;i<size;i++) {
const char *hexdigit="0123456789abcdef";
ret+=hexdigit[(data[i]>>4)&0xf]; // high 4 bits
ret+=hexdigit[(data[i] )&0xf]; // low 4 bits
}
return ret;
}
/** Example main **/
#include <iostream>
int main() {
std::cout<<"SHA256(''): "<<SHA256::digestString("").toHex()<<"\n";
std::cout<<"SHA256('a'): "<<SHA256::digestString("a").toHex()<<"\n";
return 0;
}
(Try
this in NetRun now!)
