Global Illumination Terminology: Radiology & Radiometry
2010, Dr. Lawlor, CS 481/681, CS,
UAF
So in reality, everything's
a light source. Yes, the sun is a light source. But the
sky is also a light source, filling in areas not illuminated by
direct sunlight with a soft blue glow. Your pants are a light
source, lighting up the ground in front of you with pants-colored
light.
Does this matter? Well, does this look like OpenGL?

This is an image computed using "radiosity".
Radiosity Units
The terms we'll be using to talk about light power are:
- Power carried by light
(e.g., power received at a 100% efficient photocell)
- It's not energy, but it is energy per unit time.
- Measured in Watts (=Joule / second)
- Also measured in "lumens"-- power as perceived by the human
eye. At a wavelength of 555nm, one lumen is 1/680 watt.
- AKA flux, radiant flux
- Irradiance: light
power per unit surface area leaving or arriving at a surface
- Measured in watts per square meter [of receiver or
transmitter area].
- So multiply by the receiver's area to get watts. (Assuming
everything's facing dead-on.)
- E.g., the Sun delivers an irradiance of 700W/m2
to the surface of the Earth.
- So a 10 square meter solar panel facing the sun would
receive 7000W of power.
- So a 1.0e-10 square meter CCD pixel open for 1.0e-3
seconds would receive 7.0e-11 joules of light energy, or a
couple hundred million photons (visible light photons have
energy of about 4e-19 Joules).
- Irradiance as perceived by the human eye can be measured in
"lux" (lumens per square meter).
- Radiance: "brightness"
as seen by a camera or your eye.
- Measured in (get this) watts per square meter per steradian,
or just W/m2/sr.
- See below for details on steradians, basically the total
angular size of the light source.
- Both the square meter area and steradian solid angle can
be measured at either the source or receiver, you get the
same value either way as long as you're consistent.
- Intuition: radiance is irradiance combined with direction.
- E.g., from the Earth the Sun is about half a degree across,
or about 1/120 radian, so assuming it's a tiny square it would
cover 1/14400 steradians. The radiance of the sun is
thus about 700W/m2 per 1/14400 steradians, or 10
*megawatts* per square meter per steradian (10 MW/m2/sr).
- This means if a lens sets it up so from one spot you see
the sun at a coverage of 1 steradian, that spot receives an
irradiance of 10MW/m2 of power!
- Suprisingly, radiance is unchanged along a straight line
through free space.
- That is, radiance does *not* depend directly on distance:
if the source coverage is unchanged, the radiance is
unchanged. That is, the pixel doesn't get brighter
just because the geometry is right in front of it!
- Suprisingly, radiance is even unchanged when passing
through a *lens*. Sunlight focused through a lens has
the same radiance, but because the lens changes the Sun's
*angle* (and hence solid angle coverage) of the light, the
received irradiance is bigger.
- Yes, radiance changes when light hits any non-transparent
object, like a brick.
- Solid angle: the total
angular "bigness" of light source as seen by a receiver.
- Measured in "Steradians" (abbreviated "sr").
- A light source's solid angle in steradians is defined as the
ratio of the area of the light source when projected onto the
surface of a sphere centered on the receiver. This area
is then divided by the sphere's radius squared, or
equivalently, is always performed with a unit-radius sphere.
- Examples:
- The maximum coverage is the whole sphere, which has area 4
pi * radius squared, so the maximum coverage is 4 pi
steradians.
- A hemisphere is half the sphere, so the coverage is 2 pi
steradians.
- A small square that measures T radians across covers
approximately T2 steradians. This
expression is exact for an infinitesimal square.
- A flat receiver surface only receives part of the light from
a light source low on its horizon--this is Lambert's cosine
illumination law. Hence for a flat receiver,
we've got to weight the incoming solid angle by a factor of
"cosine(angle to normal)".
- For a source that lies directly along the receiver's
normal, this doesn't affect the solid angle--it's a scaling
by 1.0.
- For a source that lies right at the receiver's horizon,
this factor totally eliminates the source's
contribution--it's a scaling by 0.0.
- For a hemisphere, this cosine factor varies across the
surface, but it integrates out to a weighted solid angle of
just 1 pi steradians (the unweighted solid angle of a
hemisphere is 2 pi steradians).
- You only want the solid angle for computing illumination
from a polygon to a point. For illumination between two
polygons, you actually want to compute the "form factor"
between the polygons, which you can either approximate using
the solid angle, or compute exactly using
Schröder
and Hanrahan's
1990 paper.
See the Light
Measurement Handbook for many more units and nice figures.
To do global illumination, we start with the radiance of each light source
(in W/m2/sr). For a given receiver patch, we
compute the cosine-weighted solid
angle of that light source, in steradians. The
incoming radiance times the
solid angle gives the
incoming irradiance (W/m2).
Most
surfaces reflect some of the light that falls on them, so some
fraction of the incoming irradiance
leaves. If the outgoing light is divided equally among all
possible directions (i.e., the surface is a diffuse or Lambertian
reflector), for a flat surface it's divided over a solid angle of pi
(cosine weighted) steradians. This means the outgoing radiance for a flat diffuse
surface is just M/pi (W/m2/sr), if the outgoing
irradiance (or radiant exitance) is M (W/m2).
To do global illumination for diffuse surfaces, then, for each
"patch" of geometry we:
- Compute how much light comes in. For each light source:
- Compute the cosine-weighted solid angle for that light
source.
- This depends on the light source's shape and position.
- It also depends on what's in the way: what shapes
occlude/shadow the light.
- Compute the radiance of the light source in the patch's
direction.
- This might just be a fixed brightness, or might depend on
view angle or location.
- Multiply the two: incoming irradiance = radiance times
weighted solid angle.
- Compute how much light goes out. For a diffuse patch,
outgoing radiance is just the total incoming irradiance (from
all light sources) divided by pi.
For a general surface, the outgoing radiance in a particular
direction is the integral, over all incoming directions, of the
product of the incoming radiance and the surface's BRDF
(Bidirectional Reflectance Distribution Function). For diffuse
surfaces, where the surface's radiance-to-radiance BRDF is just the
cosine-weighted solid angle over pi, this is computed exactly as
above.
Computing Solid Angles
So one important trick in doing this is being able to compute
cosine-weighted solid angles of light sources. Luckily, there
are several funny tricks for this.
The oldest, best-known, and least accurate way to compute a solid
angle is to assume the light source is small and/or far away.
If either of these are true, then the light source projects to a
little dot on the hemisphere, and we just need to figure out how the
area (and hence solid angle) of that dot scales with distance.
Well, the height of the dot scales like 1/z, and the width of the
dot scales like 1/z, so together the area (width times height)
scales like 1/z2. That's the old, familiar
inverse-square "law" you've heard since middle-school physics class
and which, unfortunately, is actually a lie.
First, inverse-square falloff is only valid for isotropic light sources
(same in all directions). Non-isotropic sources (think a laser
beam, or a flashlight, that shines only in one direction) don't
generally fall off this way.
Second, say the light source is an isotropic 1-meter radius disk,
sitting z meters away and directly facing you. What's the
falloff with z? It turns
out to be 1/(z2+1), not 1/z2. These are
similar for large z, but at small z the disk isn't as bright as an
equivalent point source. That is, inverse-square breaks down
when you get too close--and it's a good thing too, because you'd
reach infinite brightness at z=0!
Solid Angle from Point To Polygon Light Source
Luckily, there's a fairly simple, if bizarre, algorithm for
computing the solid angle of a polygon transmitter from any receiver
point. This algorithm was presented by Hottel and Sarofin in
1967 (for heat transfer engineering, not computer graphics!), and
again in a
1992 Graphics Gem by Filippo Tampieri.
vec3 light_vector=vec3(0.0);
for (int i=0;i<light.size();i++) { // Loop over vertices of
light source
vec3 Ri=normalize(receiver-light[i]); // Points
from light source vertex to receiver
vec3 Rp=normalize(receiver-light[i+1]); //
Points from light source's *next* vertex to receiver
light_vector += acos(dot(Ri,Rp)) *
normalize(cross(Ri,Rp));
}
float solid_angle = dot(receiver_normal,light_vector);
You can actually just dump this whole thing directly into GLSL, and
it will run. Four years ago, the "acos" kicked it out into
software rendering, which was 1000x slower. Two years ago, on
the *same* hardware, the *same* GLSL program ran in graphics
hardware, and pretty dang fast too--a sincere thank you goes out to
those unsung GLSL driver writers!
You can speed it up a bit (and mess it up too at close range!) by
first noting that
light_vector += acos(dot(Ri,Rp)) * normalize(cross(Ri,Rp))
is an angle-weighted, normalized cross product.
In theory we could compute the angle weighting just as well with
light_vector += asin(length(cross(Ri,Rp))) * normalize(cross(Ri,Rp))
This isn't actually useful in practice, because it breaks down for
nearby receivers--the angle between Ri and Rp exceeds 90 degrees,
and asin starts giving the wrong answer, while acos keeps working
all the way out to 180.
However, for distant receivers, which have small angles between Ri
and Rp, we're close to having asin x == x. Thus the above is
very nearly equal to:
light_vector += length(cross(Ri,Rp))) * normalize(cross(Ri,Rp))
Now, the length of a vector times the direction of the vector gives
the original vector, so we can actually just sum up the cross
products:
light_vector+=cross(Ri,Rp);
In practice, this is very difficult to distinguish visually from the
real equation, except very close to the light source, where this
approximation comes out a bit darker than the real thing.
Solid Angle's Achilles Heel--Occlusion
The above equation works great if the receiver can see the whole light
source. If something gets in the way of that light source, you
still compute solid angle, but only where the light source actually shines on
the receiver--a much more complicated computation to perform.
It is actually possible to clip away the occluded parts of the light
source, and then compute the solid angle of the non-occluded
pieces. I've done this in software. It's actually
tolerably fast as long as you're willing to limit yourself to a few
dozen polygons per scene. But with any realistic number of
polygons, computing the exact occluded solid angle becomes very
painfully slow. This is where approximations come in:
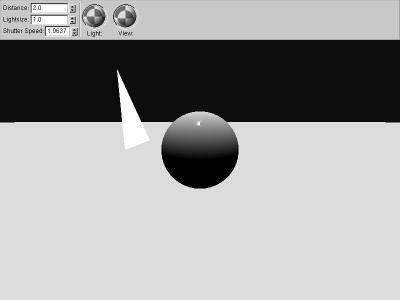 |
fixed_angle
We begin with a classic OpenGL fixed-direction,
infinite-distance light source.
|
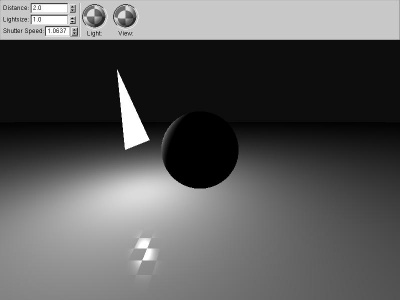 |
local_angle
If we compute the vector pointing to the light source
from each pixel, we immediately gain realism. The ground
gets darker farther away simply because the vector to the
light source is pointing farther away from the normal, not
because of any distance-related falloff.
|
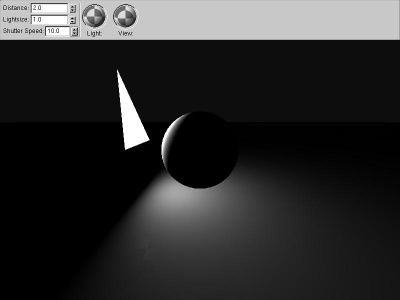 |
solid_angle
If we compute the solid angle to the actual polygon light
source, using the classic loop around the vertices
(angle-weighted cross products), we get far better local
effects, as well as properly handling light sources of
varying sizes.
|
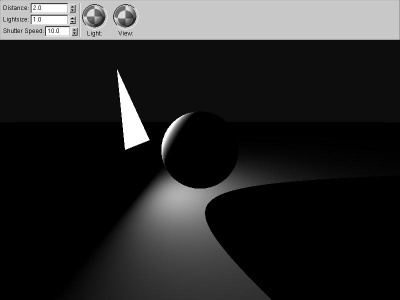 |
hard_shadow
Occluding objects cast shadows by reducing the solid
angle of the light source. The easiest way to handle this
is to shoot a ray from the receiver to the light source's
center--if the ray hits something, the object is "in
shadow". This binary shadowing choice gives clean but
unnaturally sharp shadows.
If the occluder is also a polygon, you can actually
compute the occluder's solid angle, and subtract that from
the source's solid angle. This only works if the
occluder is entirely inside the light source, from the
receiver point; otherwise you have to calculate
intersecting areas.
|
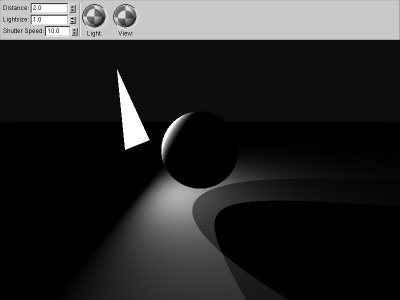 |
two_shadow
One method to approximate soft shadows is to shoot
several "shadow rays", and average the results. This is
equivalent to approximating the area light source with
several point light sources.
|
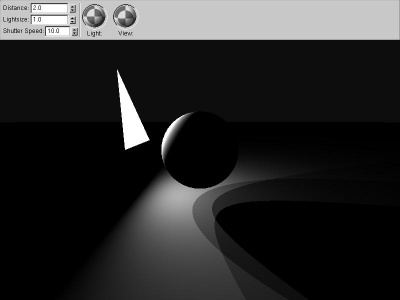 |
three_shadow
Shooting more shadow rays (in this case, three) gives a
better approximation of soft shadows, but it still isn't
really very good.
|
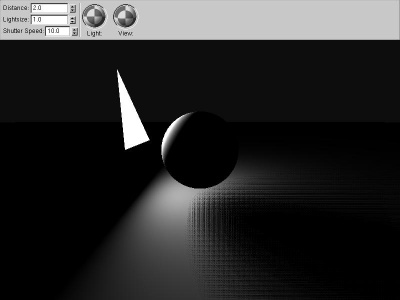 |
random_shadow
Using the same three shadow rays, but shooting toward
random points on the light source, gives far better
results. Random numbers aren't very easy to generate in a
pixel shader, so this version repeats a short series,
resulting in a rectangular dithering-type pattern. A
better approach would probably be to generate a
low-correlation random number texture, and look up the
random numbers from that.
|
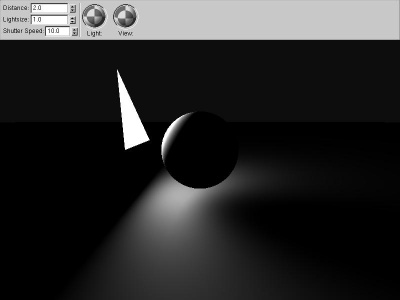 |
conetraced_shadow
For spherical light sources and occluders, you can use
"Conetracing" to estimate the fraction of the light source
covered by the occluder. The big advantage to this is you
can get analytically-accurate, smooth results while taking
only one sample. The disadvantage is it only works nicely
for spheres! I once wrote a raytracer
using conetracing for everything. Amanatides wrote
an article "Ray Tracing with Cones" in SIGGRAPH 1984
expanding how to do this correctly, and Jon Genetti has
a paper on "Pyramidal" raytracing as well.
|
Unfortunately, the Achilles heel of all these techniques is
scalability--they work fine for one or two occluders, but the
raytracing process slows down as you add occluders. A more
promising approach for even moderately large models is to somehow
use fragments to approximate solid angle and radiosity
simultaniously, which we'll look at next class.









