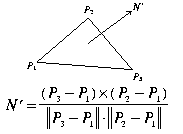
Fig. 1: Surface normal using three vertices.
With the availability of Magnetic Resonance Imaging (MRI) technology
in the medical field and the development of powerful graphics
engines in the computer world the possibility now exists for the
simulation of surgery using data obtained from an actual patient.
This paper describes a surgical simulation system which will allow a
physician or medical student to practice surgery on a patient without
ever entering an operating room.
This could substantially lower the cost of medical training by providing
an alternative to the use of cadavers.
The project involves the use of volume data acquired by MRI which
is converted to polygonal form using a corrected marching cubes
algorithm.
The data is then colored and a simulation of surface response
based on springy structures [8] is performed in real time.
Control for the system is obtained through the use of an attached
analog-to-digital unit.
A remote electronic device is described which simulates an
imaginary tool having features in common with both arthroscope
and laparoscope.
After consultation with persons in the medical profession we have decided
to build a system to simulate arthroscopic surgery on the human knee.
Of particular interest are the sports-related injuries which are becoming
more and more common. Some reasons for this decision are:
We are currently in the process of developing the surgical simulation
system described here. Our software presently runs on a Silicon Graphics
Onyx. An attached electronic device provides three dimensional input to a
real-time display program running under X and OpenGL. The simulation can
also be run on an Indigo2, provided that the workstation has sufficient
memory.
It is our intention that the initial version of the software be targeted
primarily as an educational tool for use in medical schools until any bugs
which exist can be worked out. By allowing students to practice surgery
on a simulation they can be better prepared for their first surgery on an
actual cadaver. This will also allow for the students to spend more time
practicing surgery before entering the professional world.
The simulation of surgery brings into focus problems from a broad set of
disciplines. One of the difficulties which exists is in obtaining data
appropriate for use in the simulation. Fortunately for us, physicians
already commonly employ a scanning device called a magnetic resonance
imager in diagnosing patients for arthroscopic surgery.
An MRI is a scanning device which uses electromagnetic radiation to create
a series of two-dimensional images of the human body. By placing stacks of
MRI images together we obtain a volume data set which can be used in
rendering a three-dimensional image. While the images produced by MRI
show tissues in a manner which is easily recognizable to the human eye,
the data cannot be easily interpreted by computer. Unlike Computerized
Axial Tomography (CAT) scans, the data from an MRI does not represent
tissue density but rather the quantity of residual electromagnetic
radiation present after the initial source is removed.
As the MRI data does not contain tissue type information (in any direct
sense) it is not possible for an algorithm to make a binary decision to
discern two types of tissue from one another. The solution, although
unattractive, is to have a professional radiologist "color" all of the
plates manually. By coloring, we mean that the individual must identify
all tissues on each plate and assign a value. Once this process is
completed we can proceed to a marching cubes rendering of the image.
Why use the marching cubes algorithm? In order to create a convincing
simulation we need to be able to achieve a certain frame rate in the
animation. So far, the most powerful animation hardware today requires
the use of polygonal objects. Also, the marching cubes algorithm creates
a very regular distribution of vertices which we will see later on is
useful in our animation process.
One of the problems with the marching cubes algorithm is that it does
not reliably produce correct tracing directions for the vertices in
output triangles [10]. The resultant erroneous normals produce
distracting "holes" if the image is rendered using a facet algorithm.
We present here a simple solution to this problem that fixes triangles
which were traced incorrectly by comparing their surface normals to the
gradients present in the original volume data.
We start with the general formula for computing the surface normal of
a triangle. Notice that the equation is sensitive to the direction in
which the vertices are traced. Here the trace direction determines if
the normal is heading into or out of the screen:
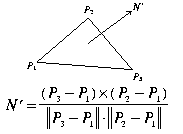
Now we look at the set of equations describing the surface normal computation using a 6-point gradient:
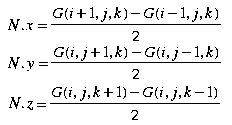
We now use the gradients to verify the trace direction for marching cubes output triangles. For each marching cubes triangle T, calculate the surface normal N' as in Figure 1 and N as in Figure 2. After normalizing both normals we take the dot product of the two and do the following:
The above technique is an after-the-fact method for repairing triangles which were traced incorrectly by the marching cubes algorithm. By making sure that all facets are traced in the right direction we will be able to use this information to calculate proper surface normals quickly during the rendering phase of animation.
One of the principal problems in simulating surgery is that the vast
medical field comes into play. There are as many surgical techniques
as there are types of injury. In order to limit our scope to a practical
level, we must think in terms of modeling the human body as opposed to
creating a system for teaching correct surgical technique. Here the
specifics of surgical tools and technique are not the issue so much as
being able to create a realistic simulation. Only after a realistic
simulation of the human body has been developed can we consider the
specific techniques of surgery.
Earlier we mentioned that we are developing an electronic data
acquisition system that will simulate features of both laparoscope and
arthroscope. Note that arthroscopes are used in surgery on the joints
while laparoscopes are used in abdominal surgery. While the arthroscope
is simply a fiber optic viewing device, some laparoscopes feature surgical
implements which are remotely controlled by the surgeon. It is these
controls which I intend to simulate with the electronic device. The
computer's monitor will serve to simulate the arthroscope's viewing
screen. The reason for this is that the remote control limits the
degrees of freedom for the user and therefore makes development of the
user interface less complex.
Why not simply simulate laparoscopic surgery? Unfortunately the tissues
involved do not show up well on either CAT or MRI scans due to the
tendency of the patient to move (breathe) while being scanned.
The process of surgery simulation has a great deal to do with animation.
Here we present a procedure for doing the simulation which should be
able to run at a good frame rate:
Every movement that the user makes in three dimensional space must
have an associated collision test to determine if a region should
become active. The problem of doing these collision tests in real
time is that we often have an large set of vertices with which to
compare. Fortunately there is a simple solution involving the use
of a three dimensional hashing function:
For every point (i,j,k) selected by the user we use the three dimensional hashing function hash to generate a pointer to the hashing table which in turn contains pointers to vertex table entries.
The hashing table was generated during the initialization phase of the program by going through the vertex table and using each vertex point as a parameter to the hashing function. The hashing table is then given an entry containing a pointer to the original vertex table entry.
Region Selection Functions (RSFs) are routines which determine the
region to become active using a starting vertex and its coloring
information. All RSFs work by spreading from the starting vertex
in all directions on the surface. By tracing edges to new vertices
we are able to prevent jumping to tissues which are near the active
region but should not be affected.
The RSFs differ in how they determine when to stop spreading out.
For example, certain types of long muscle would have an RSF that is
an oval shape oriented along the length of the muscle. Other RSFs
might describe regions whose influence is purely circular. When the
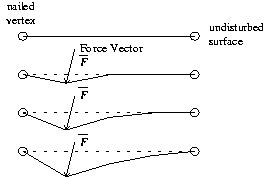
vertices being traced have spread to the boundaries they are marked
as being "nailed" for later use in the springy surface animation
algorithm. A nailed vertex will not move during the springy surface
animation. This is a necessary simplification as the springy surface
computations need to occur relatively quickly.
After a user has selected a primary vertex and has moved it from its
original position the possibility exists for a secondary vertex to come
into play. The secondary vertex in necessary to describe the effect on
the other side of a soft object when the force applied on the original
vertex has passed through the object.
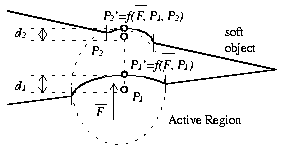
To determine a secondary vertex we draw a line from the original position of primary vertex P1 to the current position of primary vertex P1' as seen in Figure 3. The length of this line corresponds to the amount of force that the user has applied. We then extend the line by using the magnitude and sign of the applied force to determine the respective amount and direction of extension. By using preselected active regions we do effectively limit the amount of force we can simulate being applied to a vertex. This should not be a problem as it is unlikely that a surgeon will be needing to exert excessive force in the course of using the simulation.
Note that there is no absolute guarantee that the first similar surface encountered is part of a single object. However, in the case of human knee data sets it is highly probable that this secondary surface is part of the same object. The limits imposed by the region selection functions serve to further prevent uninvolved surfaces from being animated.
If the push through determiner has located a secondary vertex it then becomes necessary to add a secondary active region. This secondary active region is computed using rules similar to that of the primary active region but with one exception. The area of the secondary active region is a function of the amount of force being applied and the distance between the primary and secondary vertices.
The main engine of the simulation is a springy surface algorithm which
follows along the work of Haumann [8] at Ohio State University. In our
tissue simulation model we have two distinct sets of springs which we
are animating. The first set of springs exists along each edge in the
selected region. The individual springs are axially springy but radially
rigid. Each edge shared by two triangles forms a hinge. Unlike many
springy surface models, there is no spring holding hinged triangles in
place. We instead have springs between the current vertex positions
and their original positions. Under this model the objects being
simulated will have an affinity for their original shape. Unless a
tool is being used which calls for a permanent shape change, all
vertices will eventually return to their original configuration.
Another difference between our springy surface model and the more commonly used ones is that our vertices are massless. The scale on which the surgery is taking place is so small that tissues respond as if they had no mass at all. We are able to take advantage of this by using massless vertices to lighten the computational overhead.
For the purpose of our simulation there are essentially only three
tools which can be used. There is the probing tool which allows the
user to poke and press into an area, the clamp or grabber tool which
allows the user to both push and pull at an area, and the nibbling
tool which "removes" tissue at the specific area.
While the probe tool allows the user to push along a surface causing
dynamic reallocation of the selected regions, the grabber tool forces
the user to stay in the selected region until the grip is released.
Furthermore, the nibbling tool actually does not cut but merely pushes
vertices away from the tool. This simplification prevents us from having
to dynamically reconstruct the connections between triangular faces.
After the new vertex positions have been computed all that remains is to determine the new surface normals for the active regions and send the data to the renderer.
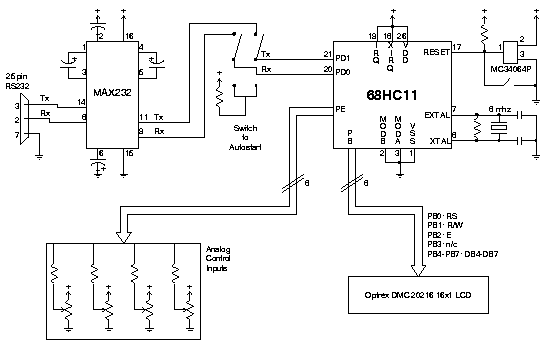
We describe a simple microcontroller circuit which can be used interface
analog controls to a host computer. Based on Motorola's 68HC11
microcontroller, the circuit described here is an eight-bit,
eight-channel analog to digital converter featuring an optional
status display. Data is sampled from up to eight independent analog
sources and is sent via serial connection to the host machine.
The device is intended to be operated in a polled mode where the host
system transmits a sample request for a particular analog device
numbered 1 through 8. The microcontroller then decodes this command,
performs the sample, and sends the resultant information back to the host.
One of the main drawbacks of the method described above is that it limits
the area which can have the spring algorithm applied to it. This
limitation is necessarily imposed due to the processing capacity of
single-CPU computer systems. However, there is the possibility of a
much more accurate simulation if all vertices could be included in the
springy surface algorithm simultaneously. With this in mind we are
working on an interface for the Cray T3D massively parallel processor
system. In this model the T3D would run springy surface calculations
while a Silicon Graphics Onyx would render the output. A high-speed
HIPPI connection between the two machines should provide enough
bandwidth to perform the simulation.
Expanded computing power might also allow for the implementation of
multiple region selection. With this we would be able to simulate
a tool interacting with a surface at more than one point. This would
increase the amount of realism in our simulation.
Another area of improvement under consideration is the use of a Gouraud
shading model. Since the only additional requirement of this model
is that we compute normals for each vertex it should be possible to
add this feature without major modification to our source code.
By using scanned data we have greatly increased the level of realism
in surgery simulation over systems which use mathematical tissue models.
In order to limit the explosive computational complexity we have at
many points opted for efficient simulation algorithms over algorithms
which produce realistic simulations. What we gain by the trade off is
a decent frame rate for our animation. A quality simulation means
nothing if the frame rate is so low that the system becomes unusable.
A wide range of expertise is needed to successfully develop a system
for the simulation of surgery. While technical problems often have
obvious solutions, these solutions do not necessarily provide for the
best possible simulation. In order for a quality system to be developed
it is necessary to do extensive consultation with medical professionals
and a review of the equipment and procedures involved.
Randy Seidlitz and G.E. medical systems for providing MRI data sets of
human knees.
Greg Schmidt and Jim Snell of Texas A&M University for their VETIT program
which allows for the coloring of MRI plates.
This research was supported in part by Cray Research, Inc. and the
Strategic Environmental Research and Development Program (SERDP) under
the sponsorship of the Army Corps of Engineers Waterways Experiment Station.