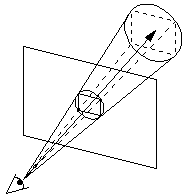
Figure 1: An eye pyray and cone.
KEYWORDS: Antialiasing, distributed light sources, object space, penumbrae, ray tracing.
The chief advantages of ray tracing are its ability to handle many different shading models, complex reflections and refractions, and many different object types. Its main disadvantages are slowness, aliasing problems and difficulties with distributed light sources. Aliasing problems result because ray tracing is a point sampling process that can only antialias frequencies below the Nyquist rate. Frequencies above the Nyquist rate result in artifacts in the image (the jaggies). In fact, any finite sampling pattern cannot guarantee no aliasing [5].
There have been several approaches to antialiasing of ray traced images. Briefly, these are: simple averaging, supersampling, stochastic sampling [3,2,4,11], and adaptive supersampling [16]. See [7,5,12] for comprehensive discussions of these topics. These approaches can be considered image-space, since it is essentially the image-space that determines if and where extra rays have to be cast. However, Whitted's adaptive supersampling [16] contains an element of the object-space approach.
We informally call an approach object-space if decisions regarding extra rays are based on information in object-space available at the time that ray-object intersections are calculated. Whitted's method calls for a sufficiently large bounding volume to surround small objects, so that rays intersecting it will be subdivided. This component of the algorithm is object-space dependent, though the rest is not. Beam tracing [9] is an object-space approach because all calculations on beams are done in object-space. Recently, there have appeared two new object-space approaches to antialiasing [15,13].
Another difficult problem for ray tracing is distributed light sources. The standard way to calculate shadows is by tracing a shadow ray to a point light source. This approach does not extend easily to distributed light sources. Beam tracing can handle such sources, but is restricted to polygonal environments. Cone tracing [1] can handle spherical light sources, but is limited to polygons and spheres. Furthermore, as shall be explained later, shadow calculations with cone tracing can be inaccurate. Stochastic sampling [3,2] handles the problem in a very time-consuming manner by distributing many rays across the light source.
In this paper, a new object-space approach to the problems of antialiasing and distributed light sources is presented. The general flavor is that of adaptive supersampling, with the difference being that decisions to subdivide are taken in object-space. This approach offers the advantages of supersampling with a computation time on par with that of adaptive supersampling. In addition, it eliminates the inherent problem with Whitted's object-space component of adaptive supersampling. Our technique also solves the problem of penumbrae from distributed light sources, producing accurate shadows. All intensity and shadow computations can be carried out to any user-prescribed degree of accuracy.
There have been three main approaches to the aliasing problem. One is to generate a fixed number of extra rays for each pixel. The second approach, a logical extension of the first, is to adaptively generate more rays for each pixel until some criterion is met. The last approach is to extend the definition of a ray - either to a different object or to allow more than one ray to be traced at a time.
In simple averaging, rays are cast at the same resolution as the screen, either through the centers or the corners of the pixels. The pixel value is then obtained as a (weighted) average of its neighboring rays. Different results are obtained by taking different neighborhoods and by varying the weights. The disadvantage of these methods is that small objects may be missed, and some jagged effects may still be seen.
In supersampling and averaging, rays are cast at a higher resolution than the screen, typically 4 to 16 rays per pixel. This method yields good results, but at a very high price in computation time. In most parts of an image, just one ray per pixel (corner) is sufficient.
Yellot [17] noticed that using an irregular sampling pattern caused featureless noise rather than false patterns and that this noise was less noticeable than false patterns. Cook [2,3] introduced the technique of stochastic sampling for antialiasing, penumbrae and motion blur. On the pixel size that he worked with, he reached the conclusion that some 16 rays per pixel produce a reasonable noise. Lee [10] and Dippé [4] further analyzed and refined the method.
Adaptive Supersampling [16] consists of casting rays through the corners of a pixel. If the 4 values do not differ from each other by too much, their average is used for the pixel. If not, more rays are cast - from the center of the pixel and the centers of the pixel edges. This subdivision continues as needed until some preset limit on the number of subdivisions is reached.
This method has a potential problem with small objects, which may escape undetected. Whitted corrects this by surrounding each small object with a bounding sphere sufficiently large so that if the object projection intersects a pixel, then at least one of the 4 rays will intersect the sphere. When this happens, the pixel is subdivided as before. We refer to this component of the algorithm as being done in object-space, because the decision to subdivide is based on information in object-space. Unfortunately, using a bounding sphere does not work well with long thin objects. The screen area in which the pixels must be subdivided unnecessarily can be very large.
Mitchell [11] used adaptive supersampling based on image-space, using Poisson-disk sampling. Painter and Sloan [14] also used adaptive supersampling based on image-space, but their procedure started from above the pixel level.
Heckbert [8] combined radiosity and ray tracing. The radiosity part, used for diffuse reflections and based on a concept of rexes, is an adaptive object-space technique, but the ray tracing part (used for specular reflections) is adaptive in image-space. This technique was implemented with point light sources.
In beam tracing [9], an initial beam is formed from the viewpoint and the view plane, and traced through the image. When a beam intersects a polygonal surface, a clipping algorithm is used to generate a reflected beam and a continuing beam. The main disadvantage is that it is limited to polygonal scenes.
In cone tracing [1], an initial cone is formed that encloses the viewpoint and the pixel. When a cone intersects the boundary of an object, the fraction of the occluded cone is calculated, and the ray is then continued past the object with a suitably reduced intensity. Although this method produces reasonable antialiasing and soft shadows, it is not accurate, because it does not account for the fact that a cone may be blocked in various orientations. Furthermore, all light sources are treated as spherical, rather than distributed.
Covers [15] are an extension of Whitted's bounding spheres. Objects are assumed surrounded by some covers of a sufficient thickness to ensure that they are intersected by a ray from at least one pixel. Thus, when a ray intersects a cover, it is in proximity to the boundary of an object, and the ray is split into two rays of reduced weight (one continues past the object, and the other hits the object). A pixel's intensity is taken as a weighted average of the two intensities. This is an object-space technique which solves some problems, but creates others. For example, covers must be quite large if one is to account for reflected rays, particularly for rays reflected off a curved surface. Furthermore, as in cone tracing, there is no distinction between different orientations of objects in a ray's path. Another problem is with thin or small objects: Since the weights are based only on the distance to the closest edge, such an object will not accurately contribute its weight to the pixel value.
In ray bound tracing [13], a ray bound surrounding the ray is used to detect the proximity of the ray to the boundary of an object. When this happens, the pixel is supersampled at some predetermined value (16 samples were used in their sample images). The drawback of this approach, as compared to adaptive methods, is that many samples are always used to capture very small or thin objects.
ASOS can be viewed as an extension of Whitted's adaptive supersampling approach carried out in object-space. The viewpoint and the pixel form a pyramid that, if extended to the end of the scene, contains any object that projects onto the pixel. We will call this a pyramidal ray or pyray for short. Since a pyramid-object intersection is very difficult to compute [1], the pyray is surrounded by a cone and a cone-object intersection is performed in two phases. Figure 1 shows an example of the initial eye pyray with dashed lines and the surrounding cone with solid lines.

Figure 1: An eye pyray and cone.
In the detection phase, a cone-object intersection is not done exactly - we simply use an in-out test like cone tracing [1] to determine if the cone intersects any part of the object. If there is no blockage of the cone, that object does not project on the pixel. If blockage is detected, an additional test is performed to determine if the blockage is total or partial. Partial blockage of the cone implies that the boundary of the object is inside the cone and the intersection is called marginal. (Note that it is possible for the object to lie in the area between the pyray and the cone). If total blockage is detected, there can be no aliasing from the boundary of this object projected on this pixel.
At the end of the detection phase, a list of all of the objects that project onto the pixel are known. If the closest object intersection is not marginal, this object covers the entire pixel and shading can be performed. In the simplest case, the central ray of the cone (which we will simply call the ray) can be used in the standard ray tracing illumination model to calculate a color for the pixel. If there is aliasing from other sources, such as texture maps or CSG intersections, any image-space method described previously can be used to reduce it at this point. In fact, additional rays can be tested faster since we know that any additional eye rays through this pixel can only strike this object.
If the closest object intersection is marginal, the pyray and its surrounding cone are called marginal and the subdivision phase is necessary. The pyray is subdivided into four pyrays, called subpyrays, and the detection phase is repeated for each subpyray. (For notational convenience, the original eye pyray is called a 0-pyray, its subpyrays are called 1-pyrays, and so on. Likewise, the central ray of a K-pyray will be called a K-ray.) This phase is not as costly, since the 4 1-pyrays only have to be tested against the list of objects that project onto the pixel, and that list has already been formed.
The decision on whether a pyray should be subdivided is also controlled by estimating an upper bound on the intensity change that could be produced by subdividing. If the estimated change is less than some user-supplied value EPS, no subdivisions are done. At this point, a color can be computed using a standard shading model with the central ray of each subpyray. This provides the user an easily controlled trade-off between image quality and processing time. Eventually, all subpyrays will be non-marginal, subdivision will become unnecessary or a user-defined limit on the number of subdivisions will be reached.
In general, assume that we have subdivided the marginal pyrays up to a level of K, so we now have to determine which (if any) of the K-pyrays need to be subdivided. Let M be the total number of marginal K-pyrays, and in (out) the number of marginal pyrays whose K-ray hits (misses) the object. Now denote L=max(in,out), and we assume for the sake of discussion that L=in.
We have two alternatives: to subdivide all the M marginal K-pyrays, or not to subdivide them. We can calculate the maximum possible change in intensity that could be produced by such a subdivision. By subdividing the L in K-pyrays, it is possible that the (K+1)-subpyrays of each of them will all be out (e.g., in the case of a thin object). This could be balanced by some of the M-L out K-pyrays spawning some (K+1)-subpyrays that are in but in the worst case, this will not happen. Since the area of every K-pyray is 1/22K, the maximum area that could be affected by the change is L/22K. If we assume intensities in the range of 0 to 1, then we see that the maximum intensity change is again just L/22K. Our decision criterion is: If L/22K <= EPS then stop subdividing the marginal pyrays.
Note that when we go from K to K+1, 22KEPS increases 4 times. Figure 2 shows a polygon that projects completely onto a pixel. Table 1 summarizes the subdivision process with EPS=1/16. Each filled circle represents a marginal 4-pyray whose 4-ray hits the polygon and each open circle represents a marginal 4-pyray whose 4-ray misses the polygon. It is interesting to note that in this example, the difference between the approximated area of the object (14 4-pyrays) and the actual area is just 0.63% of the entire area covered by the original pixel.
 Figure 2: Subdivision of a pixel. |
Table 1: Summary of Figure 2 with EPS=1/16. |
When a pyray is in proximity to just one edge, we can improve the above estimate by observing that for each marginal K-pyray, at most half of its subpyrays can switch from in to out (or from out to in). The reason is that if the K-ray of a K-pyray is in, then at most 2 of its (K+1)-subrays can be out. Therefore, in the decision criterion, L can be replaced by L/2, giving us the modified criterion of: If L/22K+1 <= EPS then stop subdividing the marginal pyrays. This would, on the average, require less subdivisions than the previous one. Figure 3 shows a pyray in proximity to just one edge and Table 2 summarizes the subdivision process for Figure 3. Now with EPS=1/16, the subdivision would stop at level 3.
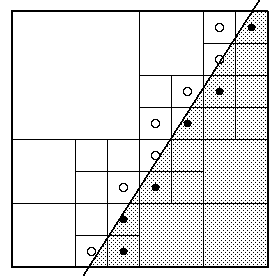 Figure 3: Pixel subdivision with one edge. |
Table 2: Summary of Figure 3 with EPS=1/16. |
Note that we should have some maximum allowable depth of subdivision so that the program does not continue subdividing in case of pathological situations. We can construct an object so that the 0-ray of the initial 0-pyray will be in, then all the 1-rays of the 1-pyrays will be out, then all the 2-rays of the 2-pyrays will be in again, and so on. We denote the maximum level by MAX, with MAX=4 sufficient for most practical purposes. This allows up to 256 4-pyrays and may produce up to 256 point samples for a pixel.
In the case of a single edge, we can easily compute an upper bound on K based on the given EPS. This can be seen by noting that no matter how the edge intersects the original 0-pyray, the maximum value for L is just 2K (the original pixel can be seen as a 2K x 2K array of K-pyrays). So in order for the modified criterion to hold, it is sufficient to have 2K <= 22K+1EPS, i.e., K >= log_2(1/EPS)-1. For example, if EPS=1/16, we will always stop with K=3 (or less, depending on L). We should further note that in a typical image, most marginal pyrays will be close to just one edge of a polygon, so we will nearly always use the modified criterion.
Since a MAX-pyray will not be subdivided, the detection phase is not necessary - the result is always a point sample. Instead of choosing the central ray, any ray inside the MAX-pyray can be point sampled. If this ray is chosen randomly, the result is a MAX x MAX jittered sample in areas of object boundaries. This effect is very dramatic in Figure 8.
Shadows from point light sources are handled as follows. When a pyray (or subpyray) hits a surface, we consider the area of intersection of the original pyray and the surface. In order to avoid aliasing, it is not enough to consider a line from the center of this area to the light and just determine if the center is in shadow or not. Instead, we consider a shadow pyray emanating from the light source and enclosing the area of intersection as shown in Figure 4. We then determine, in the manner described above, if the shadow pyray intersects any object in the path. If it does, we subdivide it in the same manner until we eventually obtain an approximation to the fraction of the area that is lit or reach the maximum level of subdivision. The level of the initial shadow pyray starts out the same as the original pyray hitting the surface. For example, if we find that a 3-pyray is not marginal we will start out the shadow pyray at level 3 and subdivide (if necessary) down to the level MAX.
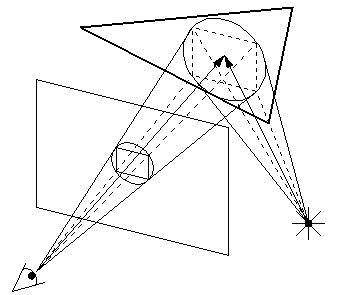
Figure 4: A shadow pyray and cone.
Shadows from rectangular light sources are handled as follows. From a surface point to be shadowed, create a shadow pyray with the point on the surface and the corners of the light as illustrated in Figure 5a. We need to find the fraction of the shadow pyray that reaches the light without being obstructed. Again, this is done as described previously for a pyray, by surrounding the pyray with a cone and the pyray splitting when it is in proximity to a boundary. The subpyrays (and their areas) that reach the light source determine the fraction of light that illuminates the point.
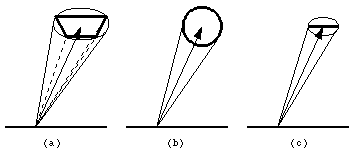
Figure 5: Distributed light sources.
The intensity of the light that we assign to each (sub)pyray hitting the light source is taken as IA cos theta, where I is the intensity of the source per unit area (assumed constant for the source), A is the area of the source subtended by the (sub)pyray, and theta is the angle between the normal of the source and the central ray of the pyray. This is the effective illumination for that particular pyray, since A cos theta is the approximate area of the projection of the subtended area on a plane perpendicular to the ray. In radiosity techniques, this is also the way that form factors are calculated [5].
Shadows from spherical light sources are handled as follows. Instead of forming a shadow pyray and then a surrounding cone, create a shadow cone directly from the spherical light source and the surface point as shown in Figure 5b. The fraction of light that reaches this point is calculated by subdividing the shadow cone. The intensity of the light that we assign to each (sub)cone hitting the light source is taken as IA. By omitting the cos theta factor, a disk perpendicular to the line of sight is simulated.
Shadows from linear light sources are handled as follows. From a surface point to be shadowed, create a shadow pyray with the point on the surface and the endpoints of the line as shown in Figure 5c. To find the fraction of the shadow pyray that reaches the linear light without being obstructed, use the same process as rectangular lights with one exception. Since a linear light is two dimensional, it is only necessary to divide a marginal shadow pyray into 2 subpyrays. For shading purposes, each point that the central ray hits on the line is treated as a point light source.
Figure 6 shows the primitives implemented and the corresponding shadows cast from each light source using ASOS(MAX=4). The upper left hand image was rendered with an antialiased point light source above the objects. The lower left hand image was rendered with a spherical light source in the same location. The upper right hand image was rendered with a linear light source parallel to the x axis. The lower right hand image was rendered with a rectangular light source in the x-z plane. Note that the penumbras of the box and cone are small for two reasons - the distance from the ground plane and the area of the light source visible. Table 3 compares the time required for cone-object intersections as opposed to ray-object intersections. A complete description of the intersection routines for these objects can be found in [6].
 |
 |
 |
 |
| primitive | Ray | Cone | Factor |
| sphere | 7.23 | 7.27 | 1.01 |
| polygon | 2.48 | 3.51 | 1.42 |
| disk | 5.68 | 5.72 | 1.01 |
| box | 4.83 | 5.75 | 1.19 |
| cone | 8.06 | 19.36 | 2.40 |
| cylinder | 6.28 | 33.98 | 5.40 |
Table 3: Cone vs. ray intersection.
Figure 8 shows 4 office scenes rendered at 1024x683 on an SGI R4000 Indigo. The upper left hand image was rendered using ASOS(MAX=3) in 41 minutes, tracing a total of 4,057,528 pyrays. The lower left hand image was also rendered with MAX=3, but with random MAX-cones in 42 minutes. The slight increase in time to calculate random MAX-cones really makes a difference - in effect this is an 8x8 stochastic sample in the penumbral areas. For comparison, the upper right image was rendered in 62 minutes using stochastic sampling with 9 rays per pixel. The lower right hand image was rendered in 111 minutes using stochastic sampling with 16 rays per pixel, tracing a total of 18,604,885 rays. Although ASOS traces less than one fourth as many "rays", the shadows look better because the extra "rays" are concentrated where they are needed.
 |
 |
 |
 |
Figure 7 shows a Victorian house made up of 2770 polygons which was rendered at 1024x683 using ASOS(MAX=4) in 147 minutes. A spherical light source provides the light and bounding boxes were used around most of the objects to speed up the intersection calculations. Figure 9 shows a frame from an animation rendered at 720x486 using ASOS(MAX=2).

Figure 7: Victorian house rendered using ASOS(MAX=4,random 4-pyrays).

Figure 9: Frame from ``Shadow of a Doubt'' rendered using ASOS(MAX=2,random 2-pyrays).
We have introduced a new technique for the aliasing problem of ray traced images and the handling of distributed light sources. ASOS operates in object-space and at any desired accuracy. The parameter EPS controls the trade-off between image quality and processing time. It allows us to guarantee the capture of arbitrarily small (or narrow) objects simply by making EPS sufficiently small. This is extremely useful in an animation, because temporal aliasing can cause small objects to flash on and off. If small objects are detected, it is important to get a good approximation to their area, because otherwise they will appear to pulsate with different intensities.
The use of our technique does not preclude the application of other antialiasing methods. In particular, it can be combined with the image-space adaptive supersampling or stochastic sampling. This combination of the two techniques can be used to handle aliasing problems not caused by the boundaries of objects. Two immediate examples of such aliasing problems are texture mapping and object intersections in CSG models.
Since shadow pyrays for distributed light sources originate from a surface point, it is possible to have shadow aliasing. This is noticeable mainly on the porch in Figure 7. It should be possible to move this point behind the surface and construct a pyray using the area of intersection as well as the light source. Any intersections between the new origin of the pyray and the surface would be ignored. A distributed light source could also be an arbitrary polygon. In fact, solving this problem would also provide a way to calculate form factors for radiosity.
In the current implementation, reflections are handled by recursively tracing the reflected ray. For flat surfaces, the eye pyray can be reflected about the surface and recursively traced if intersections between the origin of the reflected pyray and the reflecting surface are ignored. Unfortunately, the reflected pyray from a curved surface is complicated and requires further research. Likewise, refracted pyrays are also difficult to construct, especially with a distributed light source filtering through a transparent medium. The problem here is that we cannot aim a simple beam towards the light source, because of the refraction of light rays at the boundaries of the medium.
The authors wish to thank Glen Williams and Susan Van Baerle for several suggestions. Sean Graves and Russell Neper helped write the original ray tracer that was extended to include these techniques. Thanks also go out to the reviewers for their comments and suggestions.