- Recognize CFGs for most programming languages. No need to rewrite grammar.
- Most general O(n) shift-reduce method.
- Optimal syntax error detection.
- LR grammars superset of LL grammars.
Bottom-Up Parsing
- Construct parse tree from the leaves to the root.
- Corresponds to a rightmost derivation in reverse.

Rightmost derivation corresponding to Figure 4.25.
Handles during parsing of Figure 4.25.

Definition of "handle"
The leftmost simple phrase of a right-sentencial form is the handle.

Shift-Reduce Parsing
- Parser performs actions based on parse table information:
- Shift. Shift the next input symbol onto the top of the stack.
- Reduce. The right end of the string to be reduced must be at the
top of the stack. Locate the left end of the string within the stack and
decide with what nonterminal to replace the string.
- Accept. Announce successful completion of parsing.
- Error. Discover a syntax error and call an error recovery routine.
- Shift. Shift the next input symbol onto the top of the stack.
- Figure 4.28. Shift-reduce parsing on input id*id.




LR(0) Automaton
- The LR(0) automaton is a DFA which accepts viable prefixes of right sentencial forms, ending in a handle.
- States of the NFA correspond to LR(0) Items.
- Use subset construction algorithm to convert NFA to DFA.
- LR(0) Item: A grammar rule with a dot (
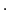 ) added between symbols on the RHS
) added between symbols on the RHS
Example: The production rule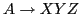 yields four items:
yields four items:
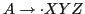
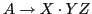
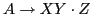
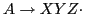
Items indicate how much of a production has been seen at a given point in parsing process.
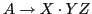 indicates a string derivable from
indicates a string derivable from 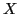 appears
on input and a string derivable from
appears
on input and a string derivable from 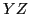 is expected on input.
is expected on input.
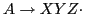 indicates input derivable from the RHS
indicates input derivable from the RHS 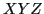 has been seen and a reduction may occur.
has been seen and a reduction may occur.
Kernel Items: All items whose dots are not at the beginning of the RHS, plus the augmented initial item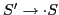 .
.
Nonkernel Items: Items with dots at beginning of RHS, except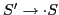 .
.
NFA of LR(0) Items: formed using each item as a state of NFA with transitions corresponding to movement of dots by one symbol.
Items with a dot preceding a nonterminal have epsilon transitions to all items beginning with that nonterminal.
LR(0) Automaton is the DFA formed by subset construction of the LR(0) NFA.
Expression grammar (4.1) produces the following LR(0) Automaton:

Nonkernel items are generated from kernel items using the closure operation
and are shown shaded.
LR(0) Parse Table
- Form NFA of LR(0) Items.
- Construct LR(0) Automaton (DFA) using subset construction.
- Construct LR Parse Table from DFA.
- LR Parse Table contains Action and GoTo sections.
- Action Table:
- If
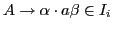 and
and
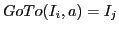 ,
for terminal
,
for terminal 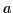 , then
, then ![$Action[i,a]$](img24.gif) = shift
= shift 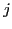 .
.
- For a complete item
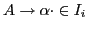 ,
,
![$Action[i,a]$](img24.gif) = reduce
= reduce
![$[A\rightarrow\alpha]$](img27.gif) for all terminals
for all terminals 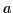 .
.
- If
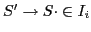 , then
, then ![$Action[i,\$]$](img29.gif) = accept.
= accept.
- If no conflicts exist in the parse table, the grammar is LR(0).
GoTo Table:
-
![$GoTo[I_i,A] = I_j$](img30.gif) becomes
becomes ![$GoTo[i,A] = j$](img31.gif) for all nonterminals
for all nonterminals 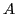 .
.
Note: The expression grammar (4.1) is not LR(0), due to shift/reduce conflicts in states 2 & 9 of the LR(0) automaton. - If
- SLR Parse Table
-
- Use Follow() set to mitigate shift/reduce conflicts.
- Step #2 in the LR(0) parse table construction is modified as follows:
- For a complete item
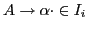 ,
,
![$Action[i,a]$](img24.gif) = reduce
= reduce
![$[A\rightarrow\alpha]$](img27.gif) for all terminals
for all terminals 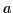 in
Follow(
in
Follow(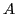 ), (
), (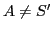 ).
).
- Note: The expression grammar (4.1) is SLR, using the parse
table in Figure 4.37.
- Figure 4.34: SLR parsing actions for input id*id.

- Ambiguous Grammars
-
- Ambiguous grammar can't be LR.
- LR proves grammar unambiguous.
- Resolve parse table conflicts by disambiguating rules.
- Control operator precedence/associativity in ambiguous grammar.
- Dangling-Else Ambiguity
Abstraction of if-then-else grammar (4.67):
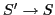
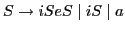

Note: Figure 4.50 is missing the item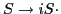 in state
in state 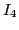 .
.
- Figure 4.51: LR parsing table for dangling-else grammar (4.67).

Note: Conflict in state 4 on input e between s5/r2 not shown.
- Figure 4.52: Parsing actions on input iiaea.

Notes:
- In step (5), (state 4, input e), s5 and r2 are both valid.
- Choosing s5 gives parse tree with e grouped with 2nd i.
- Choosing r2 gives parse tree with e grouped with 1st i.
- Resolve conflict in favor of s5, to group else with preceding
unmatched if, as shown in top parse tree in Figure 4.9.

- LR(1) Grammars
-
- Example 4.48: Abstraction of C assignment and pointer dereference
operators, grammar (4.49):

-
- Notes:
- State 2 contains shift/reduce conflict.
- Grammar is not SLR.
- Grammar is not ambiguous.
- Reduction in state 2 is not valid.
- If
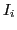 contains
contains
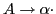 and a in Follow(A),
reduce by
and a in Follow(A),
reduce by
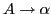 on input a.
on input a.
- But
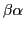 on stack may not allow
on stack may not allow 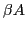 followed by a.
Thus,
followed by a.
Thus,
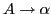 would be invalid.
would be invalid.
- Must know which terminals can follow
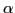 for reduction
for reduction
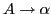 .
.
- Consider
![$[A \rightarrow \alpha \cdot B \beta, {\tt\bf a}]$](img49.gif)
- For each
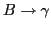 , we have
, we have
![$[B \rightarrow \cdot \gamma, {\tt\bf b}]$](img51.gif) ,
, 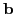 in
First(
in
First(
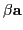 ).
).
-
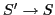
-
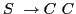
-
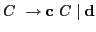
- Note: Grammar is SLR.


