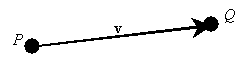CS 381  >  Week 6 Review Problems

CS 381, Fall 2003
Week 6 Review Problems

Below are some problems related to the material covered in class recently. Answers are in the Answers section, below. Do not turn these in. We may certainly discuss any of these problems in class, if you want.

You can expect Test 2 (on Friday, November 7) to contain problems similar to some of these.

Problems

Note: On the test you will be expected to do problems like these without books or notes.
  1. A weather report provides information about each of the following. Classify each as scalar, point, or vector. a. Temperature. b. Wind. c. Barometric pressure. d. Snowfall amount. e. Coldest place in the state.
     
    2. f. Historic record low.
     
  2. Very briefly, what kinds of operations make sense with a. scalars, b. vectors, and c. points?
     
  3. What kind of quantity (scalar, vector, or point) is each of the following: a. the sum of two vectors, b. the product of a scalar with a vector, c. the dot product of two vectors, d. the cross product of two (3-D) vectors.
     
  4. Suppose that P and Q are points, and u, v, and w are vectors. For each of the following statements, draw a picture that illustrates it.
    1. Q – P = v.
    2. u + v = w.

     
  5. Let u = (1, 0, –1), and let v = (2, 2, –3). Compute each of the following:
    1. u + v.
    2. u – v.
    3. –3v.
    4. u · v.
    5. u × v.
    6. |u|.
    7. |v|.
    8. Approximate the angle between u and v, in degrees, to two decimal places.

     
  6. Vector quantities have magnitude and direction. How do we represent a quantity that has only direction?
     
  7. Find the unit vector whose direction is the same as the vector w = (1, 2, 0).
     
  8. Compute the following matrix-vector products. Yes, they look ugly. Deal with it.
    1. (
       1  0  0
      0 0 –1
      0 1 0
      		) (
      2
      3
      4
      		) .
    2. (
       1  2  0
      0 1 2
      2 0 1
      		) (
      2
      3
      4
      		) .

     
  9. What 3×3 matrix represents the transformation produced by “glScaled(3, 4, 5);”?
     
  10. We can represent two of the following three 3-D transformations using 3×3 matrices, as described in class. Which one cannot be representated in that way? Why not?
     
  11. In VR, what is meant by “presence”?
     
  12. a. In VR, what is “immersion”? b. How does immersion help create a sense of presense?
     
  13. a. What is meant by “stereoscopic” (or often just “stereo”) display output? b. What important element of the human visual system is not dealt with at all by most modern stereoscopic displays?
     
  14. List the two major categories of VR display environments, and give one advantage of each over the other.
     
  15. a. In the context of VR displays, what is “latency”? b. Why does high latency produce serious problems with head-mounted VR displays, and why is this less of a problem with other displays?
     
  16. a. What is a “haptic” interface? b. In what types of environments have haptic interfaces been successfully implemented?
     

Answers

    1. Temperature: scalar.
    2. Wind: vector (includes direction & speed).
    3. Barometric pressure: scalar.
    4. Snowfall amount: scalar.
    5. Coldest place in the state: point.
    6. Historic record low: scalar.
    1. Scalars. Scalars are basically just numbers, so all the usual operations make sense with them.
    2. Vectors. Vectors can be added (and subtracted) and multiplied by scalars. There are also specialized vector operations that have no counterpart in the lower-level mathematics: magnitude, dot product, cross product (for 3-D vectors).
    3. Points. Very little can be done with points by themselves. If we deal with points and vectors together, then we can add a point and a vector, and we can subtract two points to obtain a vector.
    1. The sum of two vectors is a vector.
    2. The product of a scalar and a vector is a vector.
    3. The dot product of two scalars is a vector.
    4. The cross product of two (3-D) vectors is a (3-D) vector.
    1. Q – P = v.
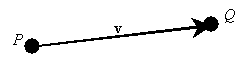
      Output of GL_LINES
    2. u + v = w.
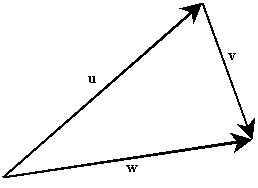
      Output of GL_LINES
    1. u + v  = (1, 0, –1) + (2, 2, 3)  = (1+2, 0+2, [–1]+3)  = (3, 2, 2).
    2. u – v  = (1, 0, –1) – (2, 2, 3)  = (1–2, 0–2, [–1]–3)  = (–1, –2, –4).
    3. –3v  = –3 (2, 2, 3)
      4.  = (–3·2, –3·2, –3·3)  = (–6, –6, –9).
    4. u · v  = (1, 0, –1) · (2, 2, 3)  = 1·2 + 0·2 + [–1]·3  = 2 + 0 + [–3]  = –1.
    5. u × v  = (0·3–[–1]·2, [–1]·2–1·3, 1·2–0·2)  = (2, –5, 2).
    6. |u|  = sqrt[12+02+[–1]2]  = sqrt[2].
    7. |v|  = sqrt[22+22+32]  = sqrt[17].
    8. The cosine of the required angle is (u · v) / (|u| |v|). We find this quanitity, then take the arccosine to obtain the angle. To find the quantity, we use the answers to parts d, f, and g: (u · v) / (|u| |v|)  = –1 / (sqrt[2] sqrt[17]) = –1 / sqrt[34]. The angle is thus arccos(–1 / sqrt[34]), or about 99.87°.
  6. We represent direction-only quantities with unit vectors. A unit vector is a vector whose magnitude is 1.
  7. The answer is w / |w|. So, first we find the magnitude: |w| = sqrt[12+22+02] = sqrt[5]. Now, w / |w| =(1/sqrt[5])·(1, 2, 0) = (1/sqrt[5], 2/sqrt[5], 0).
  8. Remember the motion: left hand moves to the right; right hand moves down.
    1. (
       1  0  0
      0 0 –1
      0 1 0
      		) (
      2
      3
      4
      		)  =  (
      1·2 + 0·3 + 0·4
      0·2 + 0·3 + [–1]·4
      0·2 + 1·3 + 0·4
      		)  =  (
      2
      –4
      3
      		) .
    2. (
       1  2  0
      0 1 2
      2 0 1
      		) (
      2
      3
      4
      		)  =  (
      1·2 + 2·3 + 0·4
      0·2 + 1·3 + 2·4
      2·2 + 0·3 + 1·4
      		)  =  (
      8
      11
      8
      		) .
  9. Here is the matrix:
    (
    3. 0. 0.
    0. 4. 0.
    0. 0. 5.
    		)
  10. We cannot represent 3-D translations with a 3×3 matrix. This is because 3-D transformations represented by such a matrix always leave the origin (0, 0, 0) in the same place. However, every translation moves the origin, except for the do-nothing (“identity”) translation that leaves every point alone.
  11. In VR, presence is the sense that one is in the computer-generated world.
    1. Immersion means filling up the user’s vision with the computer-generated world. This is generally accomplished using screens that are either very large or else right in front of the user’s eyes.
    2. Immersion helps create a sense of presence by reducing or eliminating visual stimuli from the “real world”, thus increasing the sense of being inside the virtual world.
    1. Stereoscopic displays are those that give different images to the viewer’s left and right eyes, in order to produce the illusion of depth.
    2. Most modern stereoscopic displays do not deal at all with focus. Stereo views give the illusion of depth, but all images are at the same actual distance from the eye. Thus, depth measured through differences between the images visible to the left & right eyes does not match depth measured via focus.
  14. The two major types of VR display environments are the theater-type display and the head-mounted display. Here are four advantages of the theater type: And here are four advantages of the head-mounted type:
    1. In computing in general, latency is the time between an event and the associated response. When dealing with VR displays, latency means the time it takes to update the display (with a redrawn scene).
    2. High latency can be a serious problem when using a head-mounted VR display, since, whenever the user’s head moves, the scene must be redrawn accordingly. If latency is high, then the old view of the scene appears to move with the user. This is very unrealistic and considerably lessens the sense of presence. Latency is less of a problem with displays that are not head-mounted, because the view of the scene no longer moves along with the user.
    1. Haptic interfaces are those that involve the sense of touch.
    2. Haptic interfaces have been successfully implemented in small-scale environments.

CS 381, Fall 2003: Week 6 Review Problems / Last update: 4 Nov 2002 / Glenn G. Chappell / ffggc@uaf.edu