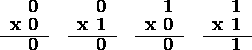
The rules for binary multiplication are:
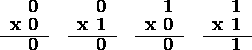
In truth table form, the multiplication of two bits, a x b is:
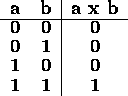
Observe that a x b is identical to the logical and operation.
Multiplication of two unsigned binary numbers, X and Y, can be performed using the longhand algorithm:
Y: 1011
X: x 101
------
1011
0000
+ 1011
--------
110111
Note that the 0 bits in X contribute a 0 to the product, while the 1 bits in X contribute Y shifted left to align with the corresponding bit in X.
The basis for the longhand algorithm can be understood from the binary representation for unsigned integers. Let X and Y be unsigned n+1 bit integers:
![]()
![]()
The product XY is given by:
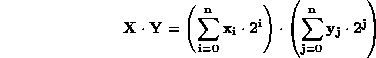
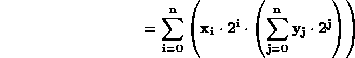
![]()
Each nonzero bit in X contributes a term consisting of Y multiplied by a power of 2.
The product of two unsigned n bit numbers can require up to 2n bits since
![]()
Overflow occurs when the product is larger than n bits.
The longhand multiplication algorithm for n bit unsigned integers can be implemented using n bit addition. Observe that the least significant bit is determined by the first term in the sum. This bit can be stored and the term can be shifted 1 bit to the right in preparation for adding the next term. This process is then repeated n times for n bits.
The longhand algorithm in SAL is:
#
# A SAL program to multiply two positive integers using addition and
# logical operations. No overflow checking is performed.
#
.data
X: .word # first number to multiply
Y: .word # second number to multiply
S: .word # the partial sum of products
I: .word # bit counter
X0: .word # rightmost bit of X
Pi: .word # i-th bit of product
P: .word # product X times Y
.text
__start:
move I, 32 # initialize counter
move S, 0 # initialize partial sum
move P, 0 # initialize result
get X # input multiplier
get Y # input multiplicand
loop: and X0, X, 1 # mask rightmost bit of X
srl X, X, 1 # shift X right 1 bit
beqz X0, shift # if x0=0, shift and get next bit
add S, S, Y # add Y to partial sum
shift: and Pi, S, 1 # mask rightmost bit of sum
or P, P, Pi # store the bit in P
srl S, S, 1 # clear sum bit from S
ror P, P, 1 # rotate P right 1 bit
sub I, I, 1 # decrement shift counter
bgtz X, loop # repeat if X nonzero
or P, P, S # combine partial sum/result
ror P, P, I # final shift
put P # output product
done
To avoid multiplicative overflow, two 32 bit integers may be multiplied to produce a 64 bit product in two 32 bit words, HI and LO, which hold the most and least significant 32 bits of the product, respectively.
In the HI/LO algorithm, multiplication is performed after splitting the 32 bit numbers to be multiplied into 16 bit HI/LO pairs and performing 32 bit multiplication on the pairs.
An implementation of the HI/LO algorithm in C language is shown below:
The 64 bit HI/LO algorithm may also be implemented in SAL:
The algorithm works without modification for a negative multiplier and a positive multiplicand. It can be extended to work for 2's complement integers. To multiply two negative numbers or a positive multiplier and negative multiplicand, two approaches are possible:
An example of method #2 applied to 4-bit 2's complement integers is shown below. The 4-bit integers 1101 (-3) and 0110 (6) are sign extended to 8 bits before multiplication. The correct result (-18) is found in the rightmost 8 bits.
11111101 (-3)
x 00000110 (6)
----------
00000000
11111101
11111101
00000000
00000000
00000000
00000000
+ 00000000
-----------------
11101110 (-18)