The division method calculates the least significant bit first.
Let D be a decimal number such that:
where 
= 0 or 1. Observe that D is even when 
= 0,
and that D is odd when = 1.
To find , divide D by 2 to obtain a quotient Q and a remainder R:
Thus, Q = D/2 and R = . Renumbering the summation, we obtain:
The least significant bit of Q is now 
. Dividing Q by 2
now produces as the remainder. The division process is repeated
on each quotient until Q = 0 to obtain all the .
The algorithm may be written in Pascal as follows:
I := 0;
Q := D;
repeat
B[I] := Q mod 2 ;
Q := Q div 2 ;
I := I + 1 ;
until Q = 0 ;
Conversion to base R is accomplished by successive divisions by R, instead of 2, in the above algorithm.
Example:
Convert 95 in base 10 to binary:
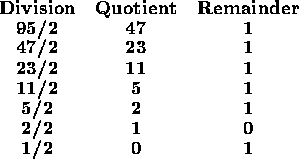
The binary representation is 1011111.