Some ratios produce a repeating pattern when converted to weighted positional notation.
Example:
The decimal fraction 1/3 = .3333.... Repeated digits are indicated
by a bar. For example, ![]() .
.
Repeating fractions occur in all bases.
Example:
Convert decimal 0.6 to binary using the multiplication method of the previous section:
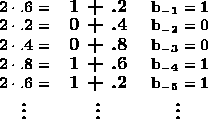
Step 5 of the conversion matches step 1 exactly. Therefore, the process will produce the same results as in the first 4 steps repeatedly and will never terminate.
The binary representation is ![]() .
.
To represent a repeating fraction exactly, the numerator and denominator must be stored as separate integers. Weighted positional numbers can be used to approximate a repeating fraction.
When a repeating proper fraction is represented using m bits,
the maximum error is ![]() .
.
Some numbers defined by mathematical equations form infinite,
non-repeating fractions. Examples are: ![]() .
.
These are called irrational numbers and can only be represented approximately in any finite representation.