So the 1980's roll on. Machines get deeper pipelines and better forwarding, until the machines usually initiate a new instruction every clock cycle. Eventually, even one cycle per instruction (CPI) is not fast enough. Sadly, one cycle per instruction is the theoretical limit of pipelining--it's the upper bound everybody's trying to reach by avoiding pipeline stalls, hazards, and flushes.
So as the 1990's arrived, designers began adding wide superscalar execution, where multiple instructions start every clock cycle. Nowadays, the metric is "instructions per cycle" (IPC), which can be substantially more than one. (Similarly, at some point travel went from gallons per mile, to miles per gallon, which is good!)
To get multiple instructions running at once, you need more than one "execution unit", so more arithmetic can execute at the same time. For example, 1994's PowerPC 601 could issue one integer, one floating-point, and one load/store instruction every clock cycle.
You can see superscalar effects in the instruction timings of any modern CPU--many instructions simply cost no time at all. For example, each these assembly programs take the exact same number of nanoseconds on my Pentium 4:
ret
(Try this in NetRun now!) -> Takes 4.4ns
mov eax,8 ret
(Try this in NetRun now!) -> Takes 4.4ns
mov ecx,7 mov eax,8 ret
(Try this in NetRun now!) -> Takes 4.4ns
mov ecx,7 mov eax,ecx ret
(Try this in NetRun now!) -> Takes 4.4ns
mov ecx,7 add eax,ecx ret
(Try this in NetRun now!) -> Takes 4.4ns
mov ecx,7 imul eax,ecx ret
(Try this in NetRun now!) -> Takes 4.4ns
add ecx,7 imul eax,ecx ret
(Try this in NetRun now!) -> Takes 4.4ns
Yet this one is actually slower by two clock cycles:
mov ecx,2 mov eax,3 mov edx,4 ret
The limiting factor for this particular instruction sequence seems to just be the number of instructions--the Pentium 4's control unit can't handle three writes per clock cycle.
You can avoid the substantial call/return overhead and see a little more timing detail using a tight loop like this one:
mov ecx,1000 start: add eax,1 dec ecx jne start ret
This takes about two clocks to go around each time. You can even add one more "add" instructions without changing the loop time (ah, superscalar!). Because the Pentium 4 uses both rising and trailing edges of the clock, a 2.8GHz Pentium 4 (like the main NetRun machine) can take half-integer multiples of the clock period, 0.357ns. So your timings are 0.357ns for one clock, 0.536ns for 1.5 clocks (like the loop above without the "add"), 0.714ns for 2.0 clocks (like the loop above), 0.893ns for 2.5 clocks, etc.
The biggest limit to superscalar execution, overall, is data dependencies: RAW, WAR, and WAW, also called "hazards." (Read it!)
| Read now | Write now | |
| Read future | RAR, not a dependency | RAW, true dependency |
| Write future | WAR, antidependency | WAW, output dependency |
You can eliminate the fake dependencies WAW and WAR using register renaming (also called Tomasulo's Algorithm): a typical implementation is to hand out a new renamed register for every write operation. Modern CPUs rename the architectural registers (like rax or rdi) out to a huge set of *hundreds* of possible physical registers. Also, because most values are passed directly arithmetic-to-arithmetic (with register bypass), today a "register" is basically just an identifier that the arithmetic units use on their internal operand forwarding network for synchronization.
Notice how if there are no writes, there are no dependencies? Functional programming extremists contend this indicates writes are evil.
Even if we allow writes, there are several interesting transformations you can use to expose and reduce dependencies, such as Software Pipelining. A naive application of these is unlikely to provide much benefit, since the compiler and CPU can do naive transformations already; but often you can exploit features of the algorithm to improve performance.
Here's the obvious way to compute the factorial of 12:
int i, fact=1;
for (i=1;i<=12;i++) {
fact*=i;
}
return fact;
Here's a modified version where we separately compute even and odd factorials, then multiply them at the end:
int i, factO=1, factE=1;
for (i=1;i<=12;i+=2) {
factO*=i;
factE*=i+1;
}
return factO*factE;
This modification makes the code "superscalar friendly", so it's possible to execute the loop's multiply instructions simultaniously. Note that this isn't simply a loop unrolling, which gives a net loss of performance, it's a higher-level transformation to expose parallelism in the problem.
| Hardware | Obvious | Superscalar | Savings | Discussion |
| Intel 486, 50MHz, 1991 |
5000ns | 5400ns | -10% | Classic non-pipelined CPU: many clocks/instruction. The superscalar transform just makes the code slower, because the hardware isn't superscalar. |
| Intel Pentium III, 1133MHz, 2002 |
59.6ns | 50.1ns | +16% | Pipelined CPU: the integer unit is fully pipelined, so we get one instruction per clock cycle. The P3 is also weakly superscalar, but the benefit is small. |
| Intel Pentium 4, 2.8Ghz, 2005 |
22.6ns | 15.0ns | +33% | Virtually all of the improvement here is due to the P4's much higher clock rate. |
| Intel Q6600, 2.4GHz, 2008 |
16.7ns | 9.4ns | +43% | Lower clock rate, but fewer pipeline stages leads to better overall performance. |
| Intel Sandy Bridge i5-2400 3.1Ghz 2011 |
11.8ns | 5.3ns | +55% | Higher clock rate and better tuned superscalar execution. Superscalar transform gives a substantial benefit--with everything else getting faster, the remaining dependencies become more and more important. |
The same trick of unrolling and breaking dependencies works for a variety of tasks. For example, this simple "add up the elements of an array" loop takes 330ns on my Skylake CPU:
const int n=1024;
int arr[n];
long foo(void) {
long sum=0;
for (int i=0;i<n;i++) {
sum+=arr[i];
}
return sum;
}
Unrolling the loop cuts the time to 245ns:
const int n=1024;
int arr[n];
long foo(void) {
long sum=0;
for (int i=0;i<n;i+=2) {
sum+=arr[i];
sum+=arr[i+1];
}
return sum;
}
We can improve the performance even more, to 196ns, by breaking the "sum" dependency chain into two halves, and only adding them together once after the entire loop:
const int n=1024;
int arr[n];
long foo(void) {
long sum0=0, sum1=0;
for (int i=0;i<n;i+=2) {
sum0+=arr[i];
sum1+=arr[i+1];
}
return sum0+sum1;
}
Repeating this unroll-and-separate approach 8 times results in 144ns:
const int n=1024;
int arr[n];
long foo(void) {
long sum0=0, sum1=0, sum2=0, sum3=0, sum4=0, sum5=0, sum6=0, sum7=0;
for (int i=0;i<n;i+=8) {
sum0+=arr[i];
sum1+=arr[i+1];
sum2+=arr[i+2];
sum3+=arr[i+3];
sum4+=arr[i+4];
sum5+=arr[i+5];
sum6+=arr[i+6];
sum7+=arr[i+7];
}
return ((sum0+sum1)+(sum2+sum3))+((sum4+sum5)+(sum6+sum7));
}
Note how we add parenthesis at the end to improve parallelism in the final summation (C++'s default is left to right associativity, which makes a sequential dependency chain through all the adds in the last line).
(We haven't hit SIMD yet, but it's faster yet to use the AVX2 SIMD instruction VPMOVSXDQ to sign-extend 4 ints into 4 longs inside a single SIMD register.)
Unrolling 16 loop iterations is slower than this, since we run out of registers to store the intermediate sum variables.
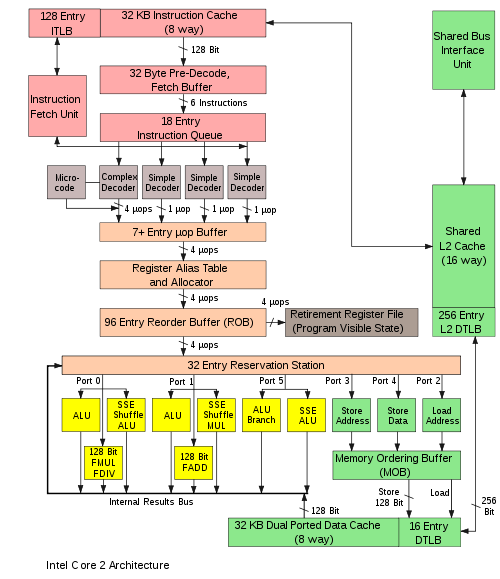
It's really interesting to watch the evolution of modern microarchitectures:

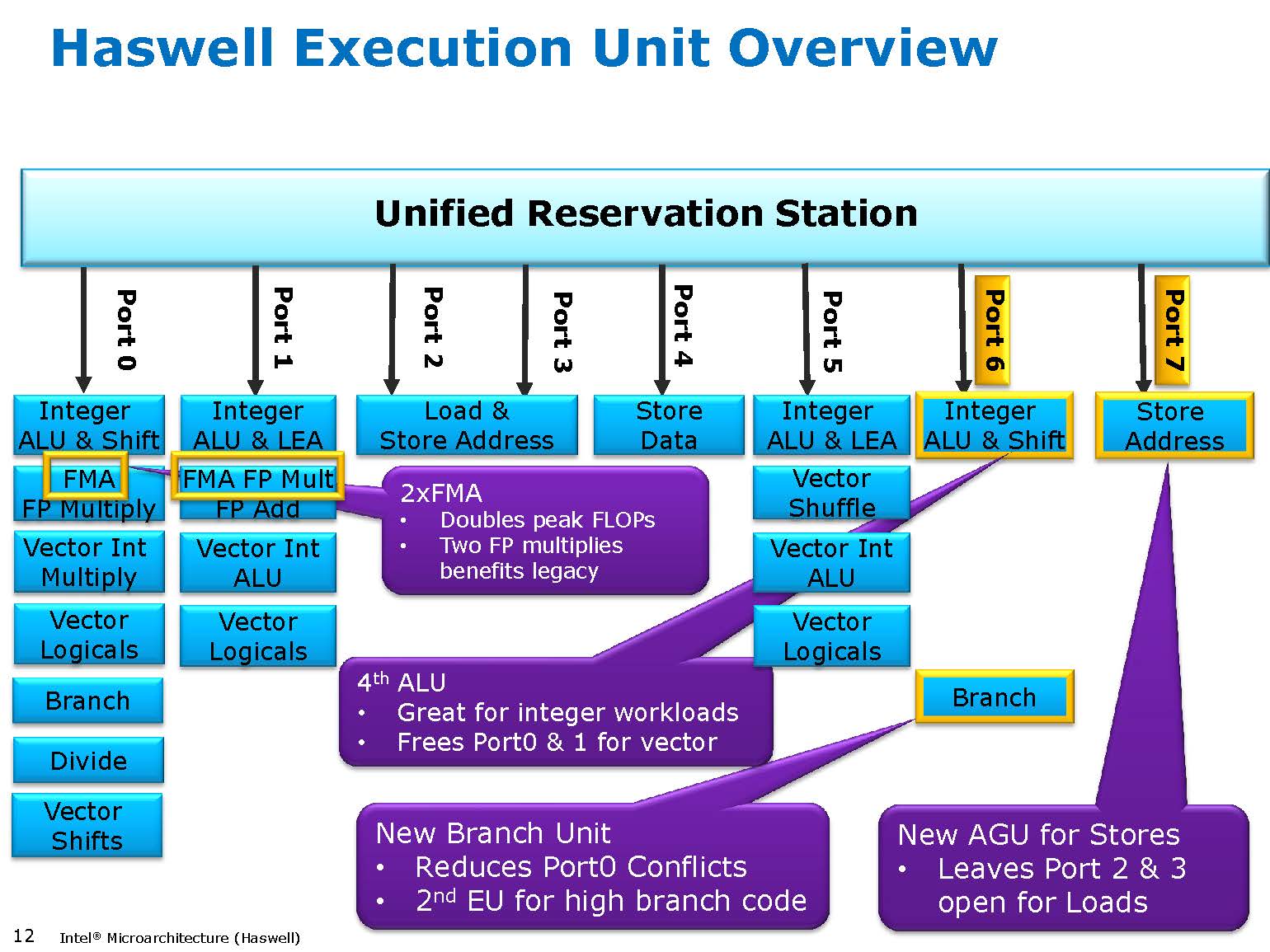
There is an inherent tradeoff between complex sophisticated features like out-of-order execution, versus the strength through numbers approach of raw parallelism (such as SIMD or multicore). Given sufficient software parallelism, out-of-order execution may not be worth the silicon area, and so may die out along with sequential software. However, some problems don't have much inherent parallelism, and so a mix of fewer more sophisticated cores (CPU) and many simpler cores (GPU) may be the approach of the future.
CS 441 Lecture Note, 2015, Dr. Orion Lawlor, UAF Computer Science Department.