Communicating Objects

CS 441/641 Lecture Notes, Dr. Lawlor

There are a variety of situations where we need to communicate entire objects:

When doing any work across the network, both the request and response are in general multi-part objects.
When reading or writing files, we often have a variety of data stored in an object.

There are essentially only two ways to store objects: fixed-size and variable-size.

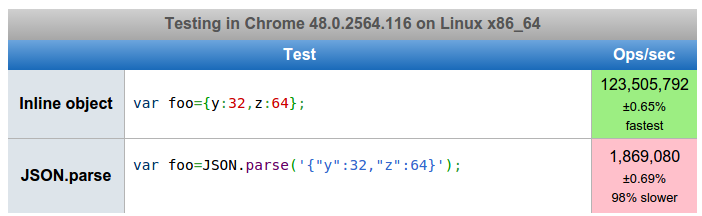
Fixed-Size Objects	Variable-Size Objects
Constant number of bytes (sizeof)	Non-constant number of bytes
C++ builtin type, class or struct Most binary file headers (e.g., BMP) Fixed-width ASCII records	C++ string, vector, map, list, ... Delimited ASCII data JSON XML
Very fast to allocate and deallocate	Surprisingly slow to allocate and deallocate (must use malloc or new)
Easy to allocate in a C++ array	Cannot be directly stored in an array (must use pointers)
Not extensible (tempted to squeeze bits)	Can be extended (though you must plan ahead!)

The speed difference between fixed and variable sized objects is enormous, mostly due to the huge overhead of allocating and deallocating variable-size memory:

template <class array_ish>
int do_the_thing(array_ish &arr) {
	arr[0]=12;
	arr[1]=34;
	return arr[0]+arr[1];
}

int do_array(void) {
	int arr[2];
	return do_the_thing(arr);
}

int do_vector(void) {
	std::vector<int> v(2);
	return do_the_thing(v);
}

void foo(void) {
	print_time("array",do_array);
	print_time("vector",do_vector);
}

(Try this in NetRun now!)

On my skylake box, this returns:

array: 1.44 ns/call
vector: 16.50 ns/call

It also stretches across many platforms, here JavaScript makes a fixed-size object inline, with good performance, or parses the same object from JSON, with terrible performance:

JavaScript object creation via inline or JSON.parse

Hybrids are also common: on a 64 bit machine a std::vector is a fixed 24 bytes, but it contains pointers to the variable-sized vector data. These pointers greatly complicate sending a std::vector across the network or storing it to a file.

Fixed-size integers lead to the frankly ridiculous problem of integer overflow when you need more bits to represent the result than are available in the integer size you have chosen. Running out of room is the classic problem with fixed-size objects, and encourages the hack of repurposing bits for other uses, such as the "0x3FFF rowBytes problem" on classic MacOS.

Fixed-size objects can be quite complex; for example even a single 32-bit float has three internal fields of different bit sizes. But since the number of bits is constant, you do get weird roundoff effects that would not be found with variable-size arithmetic, which could represent exact results.