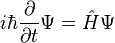Quantum Computing

CS 301: Assembly Language Programming Lecture, Dr. Lawlor

Quantum computing has gotten a ton of press, due to its enormous theoretical promise. Unfortunately, it's possible that like fusion power, which is theoretically superior to all other forms of power generation but currently intractable in practice, quantum computing is "the technology of the future, and always will be".

	Ordinary Computer	Quantum Computer
Goal	Get 'er done!	Speedups up to exponential: e.g., search n values in sqrt(n) time, factor integers in polynomial time.
Data storage	1's and 0's (bits)	Vector with axes 1 and 0 (qubits) Not just 1 or 0: both at once!
Assignments?	Yes	No (violates laws of physics)
Reversible?	No	Yes, except for "collapse" operation
Swap?	Yes	Yes
Logic gates	AND, OR, NOT	CNOT, Hadamard rotate 45 degrees
Programming Model	Instructions	Reversible Quantum Operations, and Irreversible Collapse
Clock	Square wave	Limited by coherence time
When?	Now	???
Limits	Heat & power, software	How many bits can you keep coherent?

Many things, like photons or electrons, display several very odd mechanical properties with mystical sounding quantum names. The key point here is that everything is made of waves.

The wave equation for a particle is the Schrödinger equation 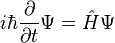$i \hbar \frac{\partial}{\partial t}\Psi = \hat H \Psi$ .

i is the usual square root of -1, since the wave phase is represented using complex numbers.
ħ ("h bar") is just a constant, the reduced Plack constant.
Ψ ("psi") is the wave itself. The probability of observing an electron at any given location is the square magnitude of the wave's amplitude. The phase of the wave isn't observable.
The interesting part is H, the Hamiltonian, which measures how much energy the particle has. If the Hamiltonian is positive, that part of the wave oscillates, changing faster with more energy. If the Hamiltonian is negative, that part of the wave dies away exponentially fast--this allows quantum tunneling.

Restating this equation in small words, "a particle's wave changes with time depending on the particle's energy."

I prepared some photographic examples of wave properties visible in laser light. Hopefully the in-class demos will work too! Waves are very strange; see IBM's atomic force microscope images of electrons bouncing off atoms, compare to the Falstad ripple tank applet (Java) for an interactive version.

IBM atomic force microscope image of electron in atom
corral

Superposition: an electron can be in several places at once, or several states at once. The terminology here is that the electron's wave function has spread over space. Needless to say, classical particles cannot do this.
Entanglement: electrons can interact. Electrons in a superposition of states can interact. Interactions between superpositioned electrons always collapse to consistent values, telling a consistent story of the electron's history. This can create surprisingly complex interactions, since the interaction of n binary unknowns represents 2ⁿ total interactions.
Collapse: if something big (e.g., a human being, a microscope, or any macroscopic measuring device) stares at the electron, it appears in exactly one place. This is called "wavefunction collapse", because the spread-out wave function bunches up again; or "state reduction", since you start with many states and end up with one state. Worse yet, it's looking less like collapse is somehow tied to an "observer", which would be merely creepy (what counts as an observer?). Delayed quantum erasure experiments mean it's probably entangling your wavefunction with the electron's, which would be freaky: just looking at the plots splits your own wavefunction into several pieces! This would mean collapse is just an illusion; what is happening is the particle's superposition has been extended to you.

A quantum computer is based on "qubits", which you can think of as a dot in 2D space: the X axis means a "0", the Y axis means a "1". Normal bits must lie on one axis or another, but qubits can live between the axes. For example,

(X,Y) coordinates (0.7,0.7) means "might be a 0, or might be a 1". Said more mystically, this is the "quantum superposition of 0 and 1". If you measure the qubit, it will randomly "collapse" to either 0 or 1.
(0.0,1.0) means "definitely a 1". If you measure the qubit, you'll always get a 1. (0.0,-1.0) actually means the same thing.
(0.3,0.95) means "it's probably a 1, but might still be 0". If you measure the qubit, you'll get a 0 10% of the time (10% = 0.3*0.3), and a 1 90% of the time (90%=0.95*0.95).

Since coordinates (0,0) means "not a 0, and not a 1", and we don't know what that means, we usually require the qubit to live on a unit sphere--it's either going to be a zero or going to be a one, so the probabilities (equal to the square of the amplitude) must add up to one.

There are many ways to implement qubits, such as via photon polarization, where "0" means horizontally polarized, "1" means vertically polarized, and a superposition is unpolarized. You could also implement the qubits as possible positions of an electron, where "0" means in the left box, "1" in the right box, and superposition means it's sitting in both boxes at once.

Tons of research groups have built single-bit quantum computers, but the real trick is entangling lots of bits together without premature "collapse", and that seems to be a lot harder to actually pull off, typically requiring the system to be electrically isolated (for example, inside a superconductor shell), mechanically isolated from vibrations, and kept near absolute zero.

Quantum Programming

Just like a classical computer uses logic gates to manipulate bits, the basic instructions in a quantum computer will use quantum logic gates to manipulate individual wavefunctions. Because you don't want to destroy any aspect of the data (this causes decoherence), these are linear operators, so you can represent any coherent quantum logic gate with a matrix that manipulates the qubit values.

1 qubit	2-entry state vector
2 qubits	4-entry state vector
3 qubits	8-entry state vector
n qubits	2ⁿ-entry state vector

One entry in a state vector is a complex number, combining amplitude, which when squared gives a probability, and a phase.

Again, think of a qubit like a little vector. One qubit is represented as a 2-entry vector representing a linear combination of the states zero |0> and one |1>. These are not exclusive, so a probability of (0.5,0.5) is a perfectly plausible qubit.

probability that qubit is 0:	magnitude of \|0>
probability that qubit is 1:	magnitude of \|1>

For example, a "Pauli-X" gate is represented by this 2x2 rotation matrix:

0	1
1	0

Plugging in the input and output coefficients, we have:

	a=0	a=1
output a=0	0	1
output a=1	1	0

The probability for a=1 on the input becomes the probability for a=0 on the output, and vice versa--this is just a NOT gate!

CNOT gate

A controlled NOT takes two bits as input. Two qubits makes a 2²=4 float vector with these components:

a=0 && b=0	\|00>
a=0 && b=1	\|01>
a=1 && b=0	\|10>
a=1 && b=1	\|11>

The CNOT gate's matrix is basically a 2x2 identity, and a 2x2 NOT gate, stuck together:

1	0	0	0
0	1	0	0
0	0	0	1
0	0	1	0

Again, putting in the input and output vectors, we can see what's going on:

	a=0		a=1
	b=0	b=1	b=0	b=1
a=0 && b=0	1	0	0	0
a=0 && b=1	0	1	0	0
a=1 && b=0	0	0	0	1
a=1 && b=1	0	0	1	0

If a=0, nothing happens--b's probabilities are exactly like before. If a=1, then b gets inverted, just like a NOT gate. If a is in a superposition of states, b is in a superposition of being inverted and not being inverted.

The basic programming model with a quantum computer is:

Initialize your quantum registers with a superposition of 0 and 1: these hence contain every possible answer.
Run a series of instructions to selectively amplify the answer you're looking for, or attenuate the answers you're not looking for. For example, you can arrange "wrong answers" so they cancel each other out. Each instruction must be a reversible operation, but in theory can be arbitrarily complex and there's no theoretical limit on the number of instructions. However, in practice, the machine only works if you can keep the whole register entangled in a coherent superposition: accidental collapse or "decoherence" is currently the limiting factor in building big quantum computers.
Finally, look at the register. The act of looking will "collapse" to a particular set of 1's and 0's, hopefully representing the right answer. If there are several right answers, physics will pick one randomly.

People started to get really interested in Quantum Computers when in 1994 Peter Shor showed a quantum computer could factor large numbers in polynomial time. The stupid algorithm for factoring is exponential (just try all the factors!), and though there are smarter subexponential algorithms known, there aren't any non-quantum polynomial time algorithms known (yet). RSA encryption, which your web browser uses to exchange keys in "https", relies on the difficulty of factoring large numbers, so cryptographers are very interested in quantum computers. In 1996, Lov Grover showed an even weirder result, that a quantum search over n entries can be done in sqrt(n) time.

Quantum Hardware

At the moment, nobody has built a popular, easy to use quantum computer, but there are lots of interesting experimental ones. The biggest number a quantum computer has factored is now 56,153 (until 2012 it was 21=3*7, after piles of science; see readable poster description of process; or try the Quantum Computing Playground version). But *if* the hardware can be scaled up, a quantum computer could solve problems that are intractable on classical computers. Or perhaps there is some physical limitation on the scale of wavelike effects--the "wavefunction collapse"--and hence quantum computers will always be limited to a too-small number of bits or too-simple circuitry. The big research area at the moment is "quantum error correction", a weird combination of physics-derived math, experimental work on optics benches, and theoretical computer science. At the moment, nobody knows if this scaling of hardware and algorithms will combine to enable useful computations anytime soon.

There's a different "Adiabatic Quantum Computer" design used by British Columbia based quantum computer company D-Wave that they hope will scale to solve some large problems. The adiabatic part of the name refers to the adiabatic theorem, proved in 1928, that says a system in quantum ground state, moved slowly (adiabatically) to a new state, is still in ground state. In practice, this allows the quantum solution of reasonably large problems, up to 1024 bits on their current hardware, but only those that fit this model and the company's choice of wiring. This is not a general-purpose quantum computer, but it has shown speedups on real-world optimization problems. They published some results in Nature (described here), and have some fairly big contracts from Amazon, Lockheed Martin, Google, etc.

Nearly every big tech company has some people working on quantum computing:

Microsoft Research started working on quantum hardware in 2004, and has been working on "topological qubits", but the only thing public so far is Language-Integrated Quantum Operations, built in the .NET language F#
Google bought an early D-Wave machine but is now talking about building their own chips, and has a Quantum Computing Playground

Thus, the future of quantum computers is currently in a superposition between two outcomes:

Y axis: Quantum computers will replace all other computers, reach and then exceed human-level intelligence, and then things will start to get really interesting.
X axis: Quantum computers will remain an interesting laboratory curiosity. Indefinitely.

This superposition may collapse sometime in the next few years. Or maybe not!