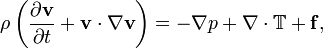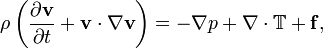Navier Stokes Fluid Dynamics

CS 482 Lecture, Dr. Lawlor

Vector Calculus: Div, Grad, Curl

For reference, you often see these vector calculus symbols in PDEs:

Symbol	Pronounced	Mathematical Definition	Input Output	Meaning
∇A	"gradient A" "grad A" or "del A"	vec3(∂A / ∂x, ∂A / ∂y, ∂A / ∂z)	scalar vector	The gradient vector points in the direction of greatest change.
∇ . A	"divergence A" or "div A"	∂A.x / ∂x + ∂A.y / ∂y + ∂A.z / ∂z	vector scalar	Positive divergence indicates areas where a vector field is leaving. Negative indicates convergence, where field is arriving.
∇ . ∇ A or ∇²A or ∆A	"laplace A" or "div grad A"	∂²A / ∂x² + ∂²A / ∂y² + ∂²A / ∂z²	scalar scalar	The Laplace operator shows up in diffusion, and other energy minimization problems.
∇ x A	"curl A" "vorticity A" or "rot A"	vec3(∂A.z / ∂y - ∂A.y / ∂z, ∂A.x / ∂z - ∂A.z / ∂x, ∂A.y / ∂x - ∂A.x / ∂y)	vector vector	The curl operator measures local rotation. The magnitude of the curl indicates rotational speed. The direction of the curl indicates the rotational axis.

Navier-Stokes Fluid Dynamics

For example, Navier-Stokes fluid dynamics is:
$navier stokes equation$

The variables here are easy enough:

v is the fluid velocity. It's a vector, and hence written in bold.
$ρ$ , the Greek letter rho, is the fluid density: mass/volume. It's there because this equation is actually "m * A = F" (rearranged F=mA).
p is the fluid pressure.
T is a stress tensor, used for viscous fluids. If viscosity is zero, you can ignore this term.
f are any other forces acting on the fluid, like gravity or wind. Calling these "body forces" makes them sound more mysterious and intimidating.

As we saw above, "∇ p" means a gradient:

∇ p = del p = vec3(∂p / dx, ∂p / dy, ∂p / ∂z)

This converts a scalar pressure, into a vector pointing in the direction of greatest change. The magnitude of the vector corresponds to the pressure difference.

We've seen this "pressure derivatives affect velocity" business in our little wave simulation program, where we're updating the current velocity:

vel.x+=dt*(L.z-R.z); /* height difference -> velocity */
vel.y+=dt*(B.z-T.z);

Written more mathematically, we're really doing this computation.

dv / dt = vec2(L.b-R.b,B.b-T.b)

Recall that from the Taylor series, we can approximate the pressure derivative with a centered difference dp/dx = (R.b-L.b)/grid_size. Say both the grid size and fluid density

ρ

both equal one. This means our simple wave simulation code is actually computing

ρ

dv / dt = vec2(L.b-R.b,B.b-T.b) = -vec2(∂p/∂x,∂p/∂y) = - del p = - ∇ p

Hey, that's exactly the leftmost terms on both sides in Navier-Stokes!

We now move on to "v · ∇ v", the term of the Navier-Stokes equations that represents moving fluid--advection, which we covered last class.

Overall, the bottom line on Navier-Stokes is actually pretty simple:
$navier stokes equation$
density * ( acceleration + advection) = pressure induced forces + viscosity induced forces + other forces