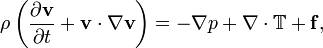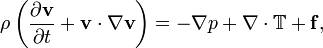Vector Partial Differential Equations & Navier-Stokes
CS 493
Lecture, Dr. Lawlor
Vector Calculus: Div, Grad, Curl
For reference, you often see these vector calculus symbols in PDEs:
Symbol
|
Pronounced
|
Mathematical Definition
|
Input
Output
|
Meaning
|
∇A
|
"gradient A"
"grad A"
or "del A" |
vec3(∂A / ∂x,
∂A / ∂y,
∂A / ∂z) |
scalar
vector
|
The gradient
vector points in the direction of greatest change.
|
| ∇ . A |
"divergence A"
or "div A" |
∂A.x / ∂x +
∂A.y / ∂y +
∂A.z / ∂z |
vector
scalar
|
Positive divergence
indicates areas where a vector field is leaving.
Negative indicates convergence, where field is arriving.
|
| ∇ . ∇ A or ∇2A
or ∆A |
"laplace A"
or
"div grad A"
|
∂2A / ∂x2 +
∂2A / ∂y2 +
∂2A / ∂z2 |
scalar
scalar
|
The Laplace
operator shows up in diffusion,
and other energy minimization problems.
|
| ∇ x A |
"curl A"
"vorticity A"
or "rot A"
|
vec3(∂A.z / ∂y - ∂A.y / ∂z,
∂A.x / ∂z - ∂A.z
/ ∂x,
∂A.y / ∂x - ∂A.x
/ ∂y) |
vector
vector
|
The curl
operator measures local rotation.
The magnitude of the curl indicates rotational speed.
The direction of the curl indicates the rotational axis.
|
Navier-Stokes Fluid Dynamics
For example, Navier-Stokes
fluid dynamics is:
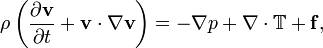
The variables here are easy enough:
- v is the fluid velocity. It's a vector, and hence
written in bold.
- ρ, the Greek letter rho, is the
fluid density: mass/volume. It's there because this
equation is
actually "m * A = F" (rearranged F=mA).
- p is the fluid pressure.
- T is a stress tensor, used for viscous fluids. If
viscosity is zero, you can ignore this term.
- f are any other forces acting on the fluid, like gravity or
wind. Calling these "body forces" makes them sound more
mysterious and intimidating.
As we saw above, "∇ p" means a gradient:
∇ p = del p = vec3(∂p / dx, ∂p
/ dy, ∂p / ∂z)
This converts a scalar pressure, into a
vector pointing in the direction of greatest change. The
magnitude of the vector corresponds to the pressure difference.
We've seen this "pressure derivatives affect velocity" business in
our
little wave simulation program, where we're updating the current
velocity:
vel.x+=dt*(L.z-R.z); /* height
difference -> velocity */
vel.y+=dt*(B.z-T.z);
Written more mathematically, we're really doing this computation.
dv / dt = vec2(L.b-R.b,B.b-T.b)
Recall that from the Taylor series, we can approximate the pressure
derivative with a centered
difference dp/dx = (R.b-L.b)/grid_size. Say both the
grid size and fluid density ρ both
equal one. This means our simple wave simulation code is
actually computing
ρ dv /
dt = vec2(L.b-R.b,B.b-T.b) = -vec2(∂p/∂x,∂p/∂y) = - del p = - ∇ p
Hey, that's exactly the leftmost terms on both sides in
Navier-Stokes!
Bulk Transport: Advection
We now move on to "v · ∇ v", the term of the Navier-Stokes
equations that represents moving fluid--this is called various
things
like convection (when driven by heat), advection (when driven by
anything else), or just "wind" or "bulk transport".
Now, "∇ v" is the gradient of the velocity: vec3( ∂v/∂x, ∂v/∂y,
∂v/∂z). This is a little odd, because velocity is already a
vector, so taking the gradient gives us a vector of vectors (a
matrix, or tensor).
Dotting this vector of vectors in "v · ∇ v" gives us a vector
again, which is good because it's being added to dv/dt, which is
also a
vector. The bottom line is:
v · ∇ v = dot(v,vec3( ∂v/∂x, ∂v/∂y,
∂v/∂z)) = v.x * ∂v/∂x + v.y * ∂v/∂y + v.z * ∂v/∂z
In English, we're dotting our vector field with its own
gradient.
This tells us how similar the vectors are to the direction of
greatest
change, which in turn says how much the value of the vector will
change
when moving in that direction. That's how "v · ∇ v"
simulates fluid transport.
Now, we could implement this by actually taking some finite
difference
approximation of ∂v/∂x and actually computing the vector v · ∇ v
at each pixel, but this approach tends to break down and go unstable
if
the velocity gets too big. The problem with the differential
approximation to transport is that it fits a linear model to the
local
velocity neighborhood; moving by more than one pixel is essentially
using linear extrapolation, which will amplify small waves in the
mesh. (The curious can read about the Courant-Fredrichs-Lewy
(CFL) condition.)
On the graphics hardware, it's
actually a lot easier to move stuff around onscreen by just changing
your texture coordinates--normally, you look "upwind" against the
flow
to see where your values are coming from:
vec4 C =
texture2D(srcTex,texCoords); /* center pixel, for vel estimate */
vec2 dir = C.xy; /* my velocity */
vec2 tc = texCoords - vel*dir; /* move "upwind" */
C = texture2D(srcTex,tc); /* advected source center pixel */
This also gives advection just like v · ∇ v, but it's more
error-tolerant than v · ∇ v, because we can advect by multiple
pixels in a single step. Jos Stam calls this technique "stable
fluids".
Overall, the bottom line on Navier-Stokes is actually pretty simple:
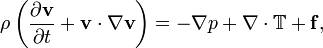
density * ( acceleration + advection) = pressure induced forces +
viscosity induced forces + other forces