Refracted Rays, Snell's Law, and Fresnel
CS 481 Lecture, Dr. Lawlor
So curiously enough, light's speed changes depending on what the
light is moving through. This speed change changes the wavelength
of the light. For example, red light has a wavelength of 650nm in
air, but the same light has a wavelength of only 260nm in diamond,
because light travels about 2.5 times more slowly through diamond than
through air.
This wavelength change has a very strange effect when light passes out
of one material and into another material. The wavelength
changes, but wave crests can't be created or destroyed at the
interface, so to make the waves match up, the light has to change direction. Here's a picture of what's going on:
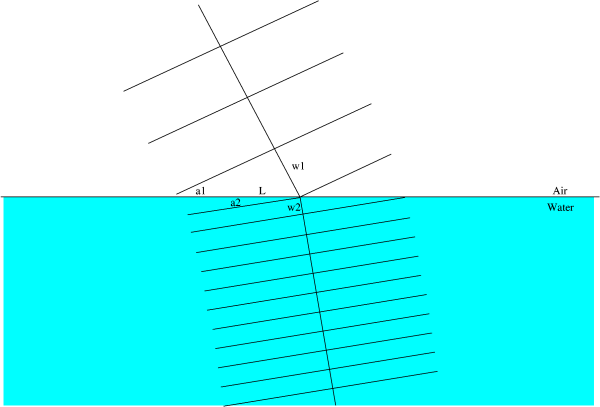
Here w1 is the wavelength in material 1, w2 is the wavelength in
material 2, L is half the width of incoming light on the surface, and
a1 and a2 are the angles between the wave fronts and the surface.
a1 and a2 are also the angles between the light direction and surface
normal!
It's just a bit of trig to figure out that
sin(a1) = w1 / L
and
sin(a2) = w2 / L
And dividing the two equalities above, we get
sin(a1)/sin(a2) = w1/w2
This is called "Snell's Law"--the ratio of sines is the ratio of
wavelengths, which is also the ratio of light speeds in the two
materials. In fact, the speed of light in air divided by the
speed of light in a material is called the material's "Index of Refraction".
A higher refractive index means slower light, smaller wavelengths, and
hence more light bending. Water's index of refraction is a mild
1.3; diamond's is a high 2.4 (this is what makes diamonds sparklier
than ice).
In a raytracer, it's easy enough to compute refraction. In GLSL,
there's even a builtin routine "refract" that takes the incoming
(camera to object) direction, surface normal, and "eta" (relative index of
refraction), and computes the refracted vector.
float eta=1.0/1.4; // air/glass's index of refraction
vec3 refractDir = refract(rayDir, hit_normal, eta);
It's easy enough
to drop this direction computation into a raytracer! About the only
tricky part is keeping track of the current index of refraction--when
you're leaving a surface (normal and ray direction point in same
direction), then you need to flip around not only the normal, but the
indicies of refraction too. A production-quality raytracer will
keep track of the index of refraction from the last-hit object, and
shoot multiple rays for a dispersive material
with different index of
refraction for each wavelength--this causes the different wavelengths
(colors) to separate out, like in a rainbow or prism.
One complication is that while exiting a more dense material, for
near-grazing angles Snell's law has no solutions because sin(a2) would
have to be greater than 1. In this case, instead of refracting
out of the material, the light reflects back into the material, called "Total Internal Reflection".
This is visible underwater, where the outside world is compressed into
a small cylinder overhead, beyond which you only see underwater objects
reflected upwards (for example, this reflected turtle). Total internal reflection is used in fiber optic cables, since it's a 100% efficient process. In a raytracer, the GLSL "refract" returns a zero-length vector in the
case of total internal reflection. You need to manually check for
this case, and fall back to reflection then.

These water droplets show refraction on top, where the light rays bend
down and hit the paper. After a wavelength-dependent transition
region, the bottom of each droplet shows total internal reflection,
where the light rays bounce off the bottom and back up into the room.
When underwater looking up,
refraction compresses the whole aboveground world into a fairly small
disk directly overhead. Outside the disk, total internal
reflection shows only the sides of the pool.
Recently, "metamaterials" using structured grids of little conductive reflectors have achieved negative index of refraction, where a wave entering from the left side refracts to the left side, instead of bending to the right at a different angle.
Fresnel Reflectance and Refractance
In addition to the direction
change when entering a new material (computed by Snell's law), there's
a brightness tradeoff between reflected and refracted light. The Fresnel formulas can be used to compute the actual relative brightness of the reflected and refracted light, but they're pretty ugly to use:
- The fresnel formulas, though physically accurate, are really slow.
- Light's
actual behavior depends on polarization, which we usually don't want to
mess with. (Though there are polarized raytracers.)
However, the overall behavior of the fresnel equations is pretty
important--the bottom line is that the steeper the incoming light
(closer to parallel to the surface, perpendicular to the normal, the
more reflection you get and the less refraction).
So there's a sort of cottage industry of "graphics-quality"
approximations to the fresnel formulas. One classic approximation
looks a heck of a lot like Phong shading--
float reflectivity=pow(1.0-clamp(dot(N,I),0.0,1.0),4.0);
That is, the reflectivity is near zero if we're looking straight down
on the surface (N and I parallel, dot product near 1); and near 1.0 if
we're looking at right angles to the surface (N and I near
perpendicular, dot product near 0).
This sort of thing is also easy to drop into a raytracer.

