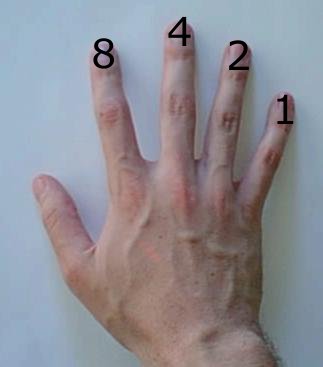
- To represent two, raise two fingers.
- To represent six, raise six fingers.
- To represent 67, grow more fingers.
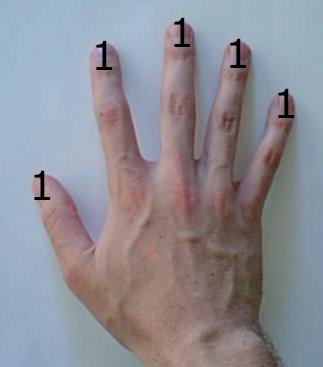
- To represent one, raise the 1 finger.
- To represent three, raise the 2 and 1 fingers together.
- To represent ten, raise the 8 and 2 fingers together.
- To represent twenty, raise the 16 (left pinky) and 4 fingers.
- To represent 67, raise the 64 (left middle finger), 2, and 1 fingers.
This is actually somewhat useful for counting--try it!
(Note: the numbers four, sixty-four, and especially sixty-eight should not be prominently displayed. Digital binary counting is not recommended in a gang-infested area.)