Machine Code: Encoding Operand Arguments
CS 641 Lecture, Dr. Lawlor
Three+ Operand Operations
RISC machines like MIPS often use three-operand operations: both source
registers and the destination register are specified. If
everything comes from a register, this doesn't actually take too many
bits--three operands at five bits each is just fifteen bits, which in a
32-bit instruction leaves plenty of room for the opcode, any constants,
padding, future expansion, etc.
For example, a MIPS add looks like this:
li $5,7
li $6,2
add $2,$5,$6
jr $31
nop
(Try this in NetRun now!)
The "add" instruction is really "a = b + c".
A RISC multiply-add instruction (a = b*c + d) is actually a four-operand operation! Both PowerPC and Itanium have multiply-adds.
Two Operand Operations
Binary operators are the most common: + - * / & | ^ <<
>>. Hence on many CISC machines such as x86, most
instructions take just two operands, and the left operand is reused as
the destination register:
mov eax,7
mov ecx,2
add eax,ecx
ret
(Try this in NetRun now!)
Here, the "add" instruction is really "a+=b".
One advantage of two-operand instructions is that you have fewer
operands, which takes fewer bits to represent. You can now use
those saved bits to add new funky addressing modes! For example,
x86 can encode all sorts of weird operand locations via the ModR/M byte.
The ModR/M byte is what allows the same add instruction above to be
used like "add eax,[ecx+edx*4+0x1959]", which accesses memory at base
address ecx plus four times edx (like an "int" array) plus a constant
offset (like a struct).
One Operand Operations
There aren't many useful unary operators: - (negate) and ~ (flip bits)
are about it. But you can actually make binary operators from
unary operators by making one operand implicit, like an accumulator
register.
Here's the (quite simple!)
instruction set for Microchip(tm) PIC microcontrollers, which are mostly one-operand instructions interacting with an accumulator named "W":
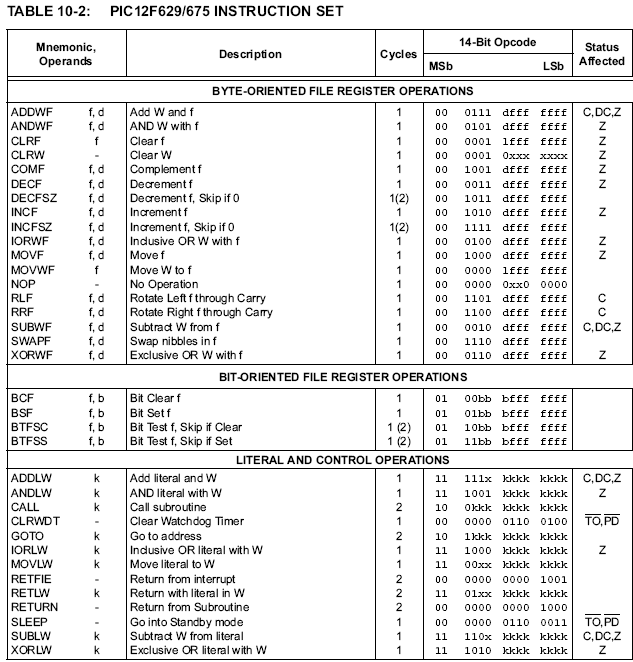
Again, "W" is the only register the machine has. "f" stands for a memory
address (up to 128 bytes). "k" stands for a program memory
address (up to 2048 instructions). "d" is the "direction bit"; it
determines whether the memory location f or the register w receives the
result.
Notice a few peculiarities of PIC micros:
- There's no hardware multiply, divide, or floating point. If you need these, you've got to write them yourself!
- Memory addresses have to be hardcoded into the instruction, which makes accessing memory via a pointer very tricky (and rare).
- Instructions
are 14 bits wide, which isn't even a multiple of 8 bits! (They're
stored in special "program memory" which is also 14 bits wide.)
If you're interested, here's the underlying PIC hardware documentation. (The table of instructions shown above is on page 72).
Here's the USB device programmer I used (with my own "usb_pickit" tool to upload the program).
Here's how to build your own circuit boards.
Zero Argument Operations: Stack Arithmetic
On many CPUs, floating-point values are usually stored in special
"floating-point registers", and are added, subtracted, etc with special
"floating-point instructions", but other than the name these registers
and instructions are exactly analogous to regular integer registers and
instructions. For example, the integer PowerPC assembly code to
add registers 1 and 2 into register 3 is "add r3,r1,r2"; the
floating-point code to add floating-point registers 1 and 2 into
floating-point register 3 is "fadd fr3,fr1,fr2".
x86 is not like that.
The problem is that the x86 instruction set wasn't designed with
floating-point in mind; they added floating-point instructions to the
CPU later (with the 8087,
a separate chip that handled all floating-point instructions).
Unfortunately, there weren't many unused opcode bytes left, and (being
the 1980's, when bytes were expensive) the designers really didn't want
to make the instructions longer. So instead of the usual
instructions like "add register A to register B", x86 floating-point
has just "add", which saves the bits that would be needed to specify
the source and destination registers!
But the question is, what the heck are you adding? The answer is
the "top two values on the floating-point register stack". That's
not "the stack" (the
memory area used by function calls), it's a separate set of values
totally internal to the CPU's floating-point hardware. There are
various load functions that push values onto the floating-point
register stack, and most of the arithmetic functions read from the top
of the floating-point register stack. So to compute stuff, you
load the values you want to manipulate onto the floating-point register
stack, and then use some arithmetic instructions.
For example, to add together the three values a, b, and c, you'd "load
a; load b; add; load c; add;". Or, you could "load a; load
b; load c; add; add;". If you've ever used an HP calculator, or
written Postscript or Forth code, you've seen this "Reverse Polish Notation". Java bytecode similarly pulls values from an operand stack, to avoid any dependence on the number of actual machine registers.
x86 Floating-Point in Practice
Here's what this looks like. The whole bottom chunk of code just
prints the float on the top of the x86 register stack, with the
assembly equivalent of the C code: printf("Yo! Here's our float:
%f\n",f);
fldpi ; Push "pi" onto floating-point stack
sub esp,8 ; Make room on the stack for an 8-byte double
fstp QWORD [esp]; Push printf's double parameter onto the stack
push my_string ; Push printf's string parameter (below)
extern printf
call printf ; Print string
add esp,12 ; Clean up stack
ret ; Done with function
my_string: db "Yo! Here's our float: %f",0xa,0
(Try this in NetRun now!)
There are lots of useful floating-point instructions:
Assembly
|
Description
|
fld1
|
Pushes into the floating-point registers the constant 1.0
|
fldz
|
Pushes into the floating-point registers the constant 0.0 |
fldpi
|
Pushes the constant pi. (Try this in NetRun now!) |
fld DWORD [eax]
|
Pushes
into the floating-point registers the 4-byte "float" loaded from memory
at address eax. This is how most constants get loaded into the
program. (Try this in NetRun now!)
|
fild DWORD [eax]
|
Pushes into the floating-point registers the 4-byte "int" loaded from memory at address eax. |
fld QWORD [eax]
|
Pushes an 8-byte "double" loaded from address eax. (Try this in NetRun now!) |
fld st0
|
Duplicates the top float, so there are now two copes of it. (Try this in NetRun now!) |
| fstp DWORD [eax] |
Pops the top floating-point value, and stores it as a "float" to address eax.
|
| fst DWORD [eax] |
Reads the top floating-point value and stores it as a "float" to address eax.
This doesn't change the value stored on the floating-point stack.
|
| fstp QWORD [eax] |
Pops the top floating-point value, and stores it as a "double" to address eax. |
faddp
|
Add the top two values, pushes the result. (Try this in NetRun now!) |
fsubp
|
Subtract the two values, pushes the result.
Note "fld A; fld B; fsubp;" computes A-B. (Try this in NetRun now!)
There's also a "fsubrp" that subtracts in the opposite order (computing B-A). |
fmulp
|
Multiply the top two values.
|
fdivp
|
Divide the top two values.
Note "fld A; fld B; fdivp;" computes A/B. (Try this in NetRun now!)
There's also a "fdivrp" that divides in the opposite order (computing B/A).
|
fabs
|
Take the absolute value of the top floating-point value.
|
fsqrt
|
Take the square root of the top floating-point value.
|
fsin
|
Take the sin() of the top floating-point value, treated as radians. (Try this in NetRun now!)
|
Remember, "stack" here means the floating-point register stack, not the memory area used for passing parameters and such.
In general, the "p" instructions pop a value from the floating-point stack.
The non-"p" instructions don't. For example, there isn't a
"fsinp" instruction, since sin only takes one argument, so the stack
stays the same height after doing a sin().
x86 has quite a few really bizarre-sounding floating-point instructions. Intel's Reference Volume 2
has the complete list (Section 3, alphabetized under "f"). The
"+1" and "-1" versions are designed to decrease roundoff, by shifting
the input to the most sensitive region.
F2XM1
|
2x - 1
|
FYL2X
|
y*log2(x), where x is on top of the floating-point stack.
|
| FYL2XP1 |
y*log2(x+1), where x is on top |
FCHS
|
-x
|
FSINCOS
|
Computes *both* sin(x) and cos(x). cos(x) ends up on top.
|
FPATAN
|
atan2(a/b), where b is on top
|
FPREM
|
fmod(a,b), where b is on top
|
FRNDINT
|
Round to the nearest integer
|
FXCH
|
Swap the top two values on the floating-point stack
|
