Partial Differential Equation Symbols, Multigrid, and Navier-Stokes
CS 480 Lecture,
Dr. Lawlor
One serious barrier to ordinary folks understanding partial differential equations is the weird symbols. For example, Navier-Stokes fluid dynamics is:
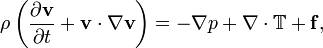
The variables here are easy enough:
- v is the fluid velocity. It's a vector, and hence written in bold.
- ρ, the Greek letter rho, is the
fluid density: volume/mass. It's there because this equation is
actually "1/m * A = F" (rearranged F=mA).
- p is the fluid pressure.
- T is a stress tensor, used for viscous fluids. If viscosity is zero, you can ignore this term.
- f are any other forces acting on the fluid, like gravity or
wind. Calling these "body forces" makes them sound more
mysterious and intimidating.
The weird part is all of the triangles ∇: these are the Greek letter nabla, an upside-down delta, which represents the del operator:
∇ = del = vec3(d _ / dx, d _ / dy, d _ / dz)
This is just a vector of derivatives along each axis--the x axis value is the derivative along x, and ditto for y and z.
You fill in the blanks with the thing you've applied del to. For example, in Navier-Stokes above, "∇ p" means:
∇ p = del p = vec3(dp / dx, dp / dy, dp / dz)
This is a "gradient": it converts a scalar, here pressure, into a vector pointing in the direction of greatest change.
We've seen this "pressure derivatives affect velocity" business in our
little wave simulation program (see
480_tex_playground/shaders/wave_velocity1.txt):
vel.x+=dt*(L.b-R.b); /* height difference -> velocity */
vel.y+=dt*(B.b-T.b);
Written more mathematically, we're really doing this computation.
dv / dt = vec2(L.b-R.b,B.b-T.b)
Recall that from the Taylor series, we can approximate the pressure derivative with a centered difference dp/dx = (R.b-L.b)/grid_size. Say both the grid size and fluid density ρ both equal one. This means our simple wave simulation code is actually computing
ρ dv / dt = vec2(L.b-R.b,B.b-T.b) = -vec2(dp/dx,dp/dy) = - del p = - ∇ p
Hey, that's exactly the leftmost terms on both sides in Navier-Stokes!
Bulk Transport: Advection
We now move on to "v · ∇ v", the term of the Navier-Stokes
equations that represents moving fluid--this is called various things
like convection (when driven by heat), advection (when driven by
anything else), "bulk transport", etc.
Now, "∇ v" is the gradient of the velocity: vec3( dv/dx, dv/dy,
dv/dz). This is a little odd, because velocity is already a
vector, so taking the gradient gives us a vector of vectors.
Dotting this vector of vectors in "v · ∇ v" gives us a vector
again, which is good because it's being added to dv/dt, which is also a
vector. The bottom line is:
v · ∇ v = dot(v,vec3( dv/dx, dv/dy, dv/dz)) = v.x * dv/dx + v.y * dv/dy + v.z * dv/dz
In English, we're dotting our vector field with its own gradient.
This tells us how similar the vectors are to the direction of greatest
change, which in turn says how much the value of the vector will change
when moving in that direction. That's how "v · ∇ v"
simulates fluid transport.
Now, we could implement this by actually taking some finite difference
approximation of dv/dx and actually computing the vector v · ∇ v
at each pixel, but this approach tends to break down and go unstable if
the velocity gets too big. On the graphics hardware, it's
actually a lot easier to move stuff around onscreen by just changing
your texture coordinates--normally, you look "upwind" against the flow
to see where your values are coming from:
vec4 C = texture2D(srcTex,texCoords); /* destination center pixel (to estimate windspeed) */
vec2 tc = texCoords - advection_scale*vec2(C); /* move "upwind" */
C = texture2D(srcTex,tc); /* advected source center pixel */
This also gives advection, but it's more error-tolerant than v · ∇ v. Jos Stam calls this technique "stable fluids".
Incompressible Fluids and Multigrid
Sometimes we don't want to deal with watching pressure waves slowly
expand and bounce around--when we push on the fluid, we want it to flow,
not to just bounce around! If the pressure is defined to be
uniform, we better make sure that the fluid velocities don't ever try
to change the pressure. Recall that pressure change is driven
from velocity divergence,
often written as "div", and defined with the del operator as "-dp / dt
= ∇ · v" (the dot is very important!). Divergence, ∇
· v, takes a vector field like velocity, and returns a scalar
field like pressure difference.
From the definition of ∇,
-dp / dt = div v = ∇ · v = dot(vec3(d _ / dx, d _ / dy, d _ / dz),v) = dv/dx + dv/dy + dv/dz
Recall that in our little simple fluid simulator,
ht+=dt*(L.r - R.r + B.g - T.g); /* velocity difference -> height */
Again, this is just a centered-difference approximation for:
dp/dt = -(dv/dx + dv/dy) = -∇ · v = -div v
Of course, our goal with incompressible fluids is to make dp/dt equal
zero; to do this, we've got to ensure the divergence of the velocity
always equals zero. One frustrating problem: by changing the
velocity at one pixel can easily force divergence to be zero there, but
this will create divergence at the neighboring pixels. This means
divergence cannot be eliminated locally, but must act across wide areas
of the mesh.
The problem of extracting a divergence-free version of a vector field is called the Helmholtz problem.
Mathematically, the cleanest way to exactly solve the Helmholtz problem
is to project the vector field to frequency space with the FFT,
drop the component of the resulting vectors that points toward the
origin, and then inverse-FFT. This works great, but it's quite
slow, especially on the graphics card.
We can more easily eliminate divergence by just computing it, and
gently penalizing it. For example, our standard shallow-water
velocity update dv / dt = - ∇ p pushes against pressure differences, so
we can reuse this to eliminate divergence. Actually... that's
what happens in the real world--at places where velocities are
converging, pressure increases, pushing back on the velocities, until
equilibrium is restored. The only trouble is this process takes
thousands of steps to redistribute velocities across a big mesh.
We can speed up pressure's normal divergence correction process by just
computing the divergence at several different spatial scales (or pixel
offsets). For example, we can easily just use "texture2DLod" to grab a
velocity sample from a higher mipmap level:
float divergence=0.0; /* magnitude of divergence of our vector field */
for (int level=levels-1;level>=0;level--) { /* loop over mipmap levels */
float size=float(1<<level); /* size, in pixels, of offset */
/* Fetch values of my neighbors on this level */
R=texture2DLod(srcTex,tc+srcDirs[0]*size,float(level));
T=texture2DLod(srcTex,tc+srcDirs[1]*size,float(level));
L=texture2DLod(srcTex,tc+srcDirs[2]*size,float(level));
B=texture2DLod(srcTex,tc+srcDirs[3]*size,float(level));
divergence+=(L.x - R.x + B.y - T.y); /* velocity difference -> divergence */
}
We can then change our velocities per-pixel to try to eliminate this
divergence, just like it was pressure (it's often called
"pseudopressure" in simulations). This goes a little bit faster
if we correct the divergence as we go, like so:
float divergence=0.0; /* magnitude of divergence of our current vector field */
vec2 velcorr=vec2(0.0); /* velocity correction for previous divergence */
for (int level=levels-1;level>=0;level--) { /* loop over mipmap levels */
float size=float(1<<level); /* size, in pixels, of offset */
/* Fetch values of my neighbors on this level */
R=texture2DLod(srcTex,tc+srcDirs[0]*size,float(level));
T=texture2DLod(srcTex,tc+srcDirs[1]*size,float(level));
L=texture2DLod(srcTex,tc+srcDirs[2]*size,float(level));
B=texture2DLod(srcTex,tc+srcDirs[3]*size,float(level));
velcorr += vec2(L.z-R.z,B.z-T.z); /* divergence difference -> velocity */
divergence+=(L.x - R.x + B.y - T.y); /* velocity difference -> divergence */
}
vel+=dt*velcorr; /* divergence difference -> velocity */
gl_FragColor = vec4(vel.x,vel.y,divergence,1.0); /* output color, for next step */
This seems to work quite well with a dt of 0.03, beyond which we go unstable.
One final and curious correction is to note that our divergence
elimination process is actually throwing away energy from the vector
field, by pushing back on regions of high divergence. Since
vortices or eddies are often regions of high divergence, this has the
effect of damping out vorticies from the flow. One clever idea is
to re-inject our velocity correction after rotation by 90 degrees--this
won't affect divergence, but keeps vortices from draining away:
vel+=dt*velcorr; /* divergence difference -> velocity */
/* now put back in some of the energy we destroyed */
vec2 vortexForce = vortex*vec2(-velcorr.y,velcorr.x); /* 90 degrees to velcorr */
if (dot(vortexForce,vel)<0) vortexForce=-vortexForce; /* push in velocity's direction */
vel+=dt*vortexForce;
This works well to maintain vortices at a "vortex" parameter of about
0.1. See 480_multigrid_fluid for an executable example.