Encoding Arguments in Machine Code

CS 441 Lecture, Dr. Lawlor

Review: x86 machine code in 301 lecture notes. amd64 cheat sheet.

AMD's 64-bit x86 Extensions

Around 2003, AMD released a set of extensions to the x86 machine code that fixed these longstanding bugs:

x86 is 32-bit, but that only lets you access 4GB of RAM at a time. Machines from Walmart now regularly exceed this amount.
x86 only has 8 registers, which isn't enough for most function's local variables.

AMD's solution was quite clever. They added a "prefix byte" that allows the next instruction to run in 64-bit mode, or use a total of 16 registers:

AMD64 Prefix Byte:

The m bit is 1 for a 64-bit operation, 0 for a 32-bit operation.
The a bit gives the high bit of the first register number. The low three bits come from the subsequent instruction as usual.
The b bit similarly gives the high bit of the second register, if one is used in the next instruction.
The c bit is the high bit of the third register number.

For example, "0x48" is a prefix byte indicating the next operation is 64-bit, normal registers.
"0x41" indicates 32-bit mode, but the first register number's highest bit is set.

For example,

"0xba <32-bit constant>" loads a 32-bit constant into register 2 (binary 010).
"0x41 0xba <32-bit constant>" loads a 32-bit constant into register 10 (binary 1010).
"0x48 0xba <64-bit constant>" loads a 64-bit constant into register 2.
"0x49 0xba <64-bit constant>" loads a 64-bit constant into register 10.

In 32-bit mode, the "0x4..." instructions were nearly-useless increment and decrement instructions. AMD repurposed them to extend the arithmetic and register set of x86 in a way that was nearly 100% backwards compatible, both with existing machine code and instruction decode circuitry!

Three+ Operand Operations

RISC machines like MIPS often use three-operand operations: both source registers and the destination register are specified. If everything comes from a register, this doesn't actually take too many bits--three operands at five bits each is just fifteen bits, which in a 32-bit instruction leaves plenty of room for the opcode, any constants, padding, future expansion, etc.

For example, a MIPS add looks like this:

li $5,7
li $6,2
add $2,$5,$6
jr $31
nop

(Try this in NetRun now!)

The "add" instruction is really "a = b + c".

A RISC multiply-add instruction (a = b*c + d) is actually a four-operand operation! Both PowerPC and Itanium have multiply-adds.

Two Operand Operations

Binary operators are the most common: + - * / & | ^ << >>. Hence on many CISC machines such as x86, most instructions take just two operands, and the left operand is reused as the destination register:

mov eax,7
mov ecx,2
add eax,ecx
ret

(Try this in NetRun now!)

Here, the "add" instruction is really "a+=b".

One advantage of two-operand instructions is that you have fewer operands, which takes fewer bits to represent. You can now use those saved bits to add new funky addressing modes! For example, x86 can encode all sorts of weird operand locations via the ModR/M byte. The ModR/M byte is what allows the same add instruction above to be used like "add eax,[ecx+edx*4+0x1959]", which accesses memory at base address ecx plus four times edx (like an "int" array) plus a constant offset (like a struct).

One Operand Operations

There aren't many useful unary operators: - (negate) and ~ (flip bits) are about it. But you can actually make binary operators from unary operators by making one operand implicit, like an accumulator register.

Here's the (quite simple!) instruction set for Microchip(tm) PIC microcontrollers, which are mostly one-operand instructions interacting with an accumulator named "W":
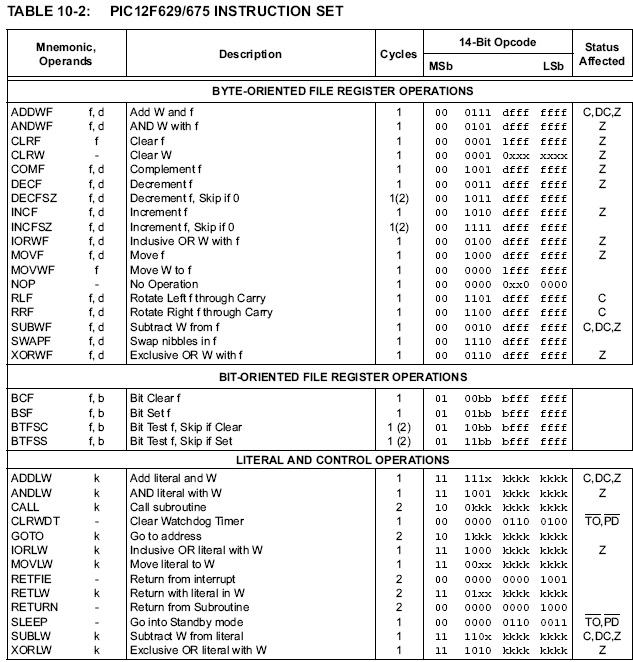
Instruction set for PIC microcontrollers

Instruction set for PIC microcontrollers

Again, "W" is the only register the machine has. "f" stands for a memory address (up to 128 bytes). "k" stands for a program memory address (up to 2048 instructions). "d" is the "direction bit"; it determines whether the memory location f or the register w receives the result.

Notice a few peculiarities of PIC micros:

There's no hardware multiply, divide, or floating point. If you need these, you've got to write them yourself!
Memory addresses have to be hardcoded into the instruction, which makes accessing memory via a pointer very tricky (and rare).
Instructions are 14 bits wide, which isn't even a multiple of 8 bits! (They're stored in special "program memory" which is also 14 bits wide.)

If you're interested, here's the underlying PIC hardware documentation. (The table of instructions shown above is on page 72). Here's the USB device programmer I used (with my own "usb_pickit" tool to upload the program). Here's how to build your own circuit boards.

Zero Argument Operations: Stack Arithmetic

On many CPUs, floating-point values are usually stored in special "floating-point registers", and are added, subtracted, etc with special "floating-point instructions", but other than the name these registers and instructions are exactly analogous to regular integer registers and instructions. For example, the integer PowerPC assembly code to add registers 1 and 2 into register 3 is "add r3,r1,r2"; the floating-point code to add floating-point registers 1 and 2 into floating-point register 3 is "fadd fr3,fr1,fr2".

x86 is not like that.

The problem is that the x86 instruction set wasn't designed with floating-point in mind; they added floating-point instructions to the CPU later (with the 8087, a separate chip that handled all floating-point instructions). Unfortunately, there weren't many unused opcode bytes left, and (being the 1980's, when bytes were expensive) the designers really didn't want to make the instructions longer. So instead of the usual instructions like "add register A to register B", x86 floating-point has just "add", which saves the bits that would be needed to specify the source and destination registers!

But the question is, what the heck are you adding? The answer is the "top two values on the floating-point register stack". That's not "the stack" (the memory area used by function calls), it's a separate set of values totally internal to the CPU's floating-point hardware. There are various load functions that push values onto the floating-point register stack, and most of the arithmetic functions read from the top of the floating-point register stack. So to compute stuff, you load the values you want to manipulate onto the floating-point register stack, and then use some arithmetic instructions.

For example, to add together the three values a, b, and c, you'd "load a; load b; add; load c; add;". Or, you could "load a; load b; load c; add; add;". If you've ever used an HP calculator, or written Postscript or Forth code, you've seen this "Reverse Polish Notation". Java bytecode similarly pulls values from an operand stack, to avoid any dependence on the number of actual machine registers.

x86 Floating-Point in Practice

Here's what this looks like. The whole bottom chunk of code just prints the float on the top of the x86 register stack, with the assembly equivalent of the C code: printf("Yo! Here's our float: %f\n",f);

fldpi ; Push "pi" onto floating-point stack

sub esp,8 ; Make room on the stack for an 8-byte double
fstp QWORD [esp]; Push printf's double parameter onto the stack
push my_string ; Push printf's string parameter (below)
extern printf
call printf  ; Print string
add esp,12    ; Clean up stack

ret ; Done with function

my_string: db "Yo!  Here's our float: %f",0xa,0

(Try this in NetRun now!)

There are lots of useful floating-point instructions:

Assembly	Description
fld1	Pushes into the floating-point registers the constant 1.0
fldz	Pushes into the floating-point registers the constant 0.0
fldpi	Pushes the constant pi. (Try this in NetRun now!)
fld DWORD [eax]	Pushes into the floating-point registers the 4-byte "float" loaded from memory at address eax. This is how most constants get loaded into the program. (Try this in NetRun now!)
fild DWORD [eax]	Pushes into the floating-point registers the 4-byte "int" loaded from memory at address eax.
fld QWORD [eax]	Pushes an 8-byte "double" loaded from address eax. (Try this in NetRun now!)
fld st0	Duplicates the top float, so there are now two copes of it. (Try this in NetRun now!)
fstp DWORD [eax]	Pops the top floating-point value, and stores it as a "float" to address eax.
fst DWORD [eax]	Reads the top floating-point value and stores it as a "float" to address eax. This doesn't change the value stored on the floating-point stack.
fstp QWORD [eax]	Pops the top floating-point value, and stores it as a "double" to address eax.
faddp	Add the top two values, pushes the result. (Try this in NetRun now!)
fsubp	Subtract the two values, pushes the result. Note "fld A; fld B; fsubp;" computes A-B. (Try this in NetRun now!) There's also a "fsubrp" that subtracts in the opposite order (computing B-A).
fmulp	Multiply the top two values.
fdivp	Divide the top two values. Note "fld A; fld B; fdivp;" computes A/B. (Try this in NetRun now!) There's also a "fdivrp" that divides in the opposite order (computing B/A).
fabs	Take the absolute value of the top floating-point value.
fsqrt	Take the square root of the top floating-point value.
fsin	Take the sin() of the top floating-point value, treated as radians. (Try this in NetRun now!)

Remember, "stack" here means the floating-point register stack, not the memory area used for passing parameters and such.

In general, the "p" instructions pop a value from the floating-point stack.

The non-"p" instructions don't. For example, there isn't a "fsinp" instruction, since sin only takes one argument, so the stack stays the same height after doing a sin().

x86 has quite a few really bizarre-sounding floating-point instructions. Intel's Reference Volume 2 has the complete list (Section 3, alphabetized under "f"). The "+1" and "-1" versions are designed to decrease roundoff, by shifting the input to the most sensitive region.

F2XM1	2^x - 1
FYL2X	y*log₂(x), where x is on top of the floating-point stack.
FYL2XP1	y*log₂(x+1), where x is on top
FCHS	-x
FSINCOS	Computes both sin(x) and cos(x). cos(x) ends up on top.
FPATAN	atan2(a/b), where b is on top
FPREM	fmod(a,b), where b is on top
FRNDINT	Round to the nearest integer
FXCH	Swap the top two values on the floating-point stack