Digital Binary Computation with Fingers and Circuits

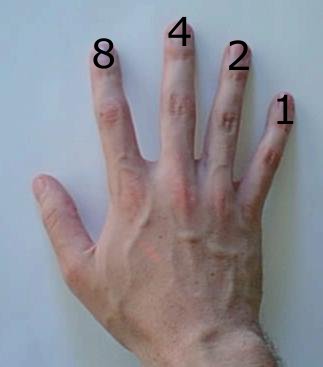
So here's normal, base-1 counting on your fingers.  In base 1, you just raise the number of fingers equal to the value you're trying to represent: To represent two, raise two fingers. To represent six, raise six fingers. To represent 67, grow more fingers.

This is funky base-2 counting on your fingers. Each finger represents a different value now, so you have to start counting with '1' at your pinky, then '2' with just your ring finger, and '3=2+1' is pinky and ring finger together. '4' is a single raised middle finger. Then '5=4+1' is middle finger and pinky, and so on. Just 10 digits actually allows you to count all the way to 1023, but we'll ignore the thumbs and just use 8 fingers, to count up to 255=128+64+32+16 (left hand palm-up, pinky is 16) +8+4+2+1 (right hand palm-down, pinky is 1). 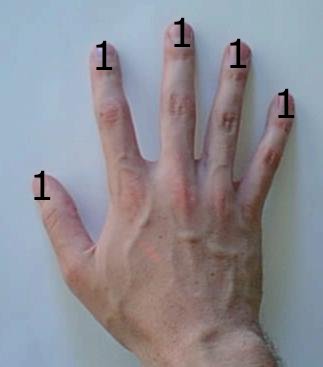To represent one, raise the 1 finger. To represent three, raise the 2 and 1 fingers together. To represent ten, raise the 8 and 2 fingers together. To represent twenty, raise the 16 (left pinky) and 4 fingers. To represent 67, raise the 64 (left middle finger), 3, and 1 fingers. This is actually somewhat useful for counting--try it! (Note: the numbers four, sixty-four, and especially sixty-eight should not be prominently displayed.  Digital binary counting is not recommended in a gang-infested area.)