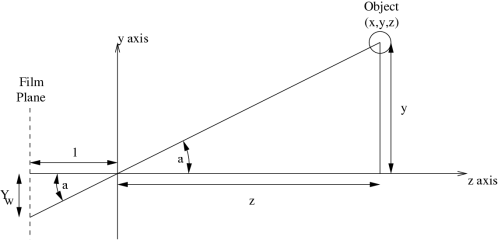
Here's a cross-section (along the x==0 plane) of a simple 3D projection setup. The camera's aperture is centered at the origin, facing in the +z direction. It's looking at an object at coordinates (x,y,z), where x is zero and z is positive. The image is focused onto a film plane at z==-1, one unit away from the origin, where the image sits at coordinate Yw (Y in the film window).

The question is, what's the equation for Yw in terms of y and z? Please write the mathematical equation on a sheet of paper. Due in class on Tuesday, September 5th.
The answer can be found by looking at the angle "a" above. I claim it's the same angle on the object side of the origin as on the film side (they're "vertical angles"). Because the axes and film are at right angles, we've got two right triangles. Then if we look at the object triangle,
tan(a) = y / z
And if we look at the film triangle
tan(a) = Yw / 1
And since these two are equal,
Yw / 1 = y / z
Or
Yw = y / z
This is the equation we're looking for--divide by Z for perspective. You can also reach this same conclusion by similar triangles. See Chapter 1.4 of the Angel book for another derivation.