Multiplication

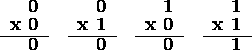
The rules for binary multiplication are:

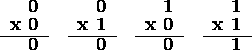
In truth table form, the multiplication of two bits, a x b is:

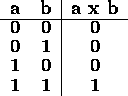
Observe that a x b is identical to the logical and operation.

Multiplication of two unsigned binary numbers, X and Y, can be performed using the longhand algorithm:

Y:   1011
X:  x 101
   ------
     1011
    0000
 + 1011
 --------
   110111

Note that the 0 bits in X contribute a 0 to the product, while the 1 bits in X contribute Y shifted left to align with the corresponding bit in X.

The basis for the longhand algorithm can be understood from the binary representation for unsigned integers. Let X and Y be unsigned n+1 bit integers:

The product XY is given by:

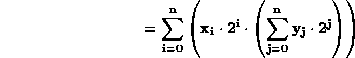
Each nonzero bit in X contributes a term consisting of Y multiplied by a power of 2.

The product of two unsigned n bit numbers can require up to 2n bits since

Overflow occurs when the product is larger than n bits.

The longhand multiplication algorithm for n bit unsigned integers can be implemented using n bit addition. Observe that the least significant bit is determined by the first term in the sum. This bit can be stored and the term can be shifted 1 bit to the right in preparation for adding the next term. This process is then repeated n times for n bits.

The longhand algorithm in SAL is:

#
#       A SAL program to multiply two positive integers using addition and
#       logical operations.  No overflow checking is performed.
#
        .data
X:      .word    # first number to multiply
Y:      .word    # second number to multiply
S:      .word    # the partial sum of products
I:      .word    # bit counter
X0:     .word    # rightmost bit of X
Pi:     .word    # i-th bit of product
P:      .word    # product X times Y

        .text
__start:
        move    I, 32            # initialize counter
        move    S, 0             # initialize partial sum
        move    P, 0             # initialize result
        get     X                # input multiplier
        get     Y                # input multiplicand
loop:   and     X0, X, 1         # mask rightmost bit of X
        srl     X, X, 1          # shift X right 1 bit
        beqz    X0, shift        # if x0=0, shift and get next bit
        add     S, S, Y          # add Y to partial sum
shift:  and     Pi, S, 1         # mask rightmost bit of sum
        or      P, P, Pi         # store the bit in P
        srl     S, S, 1          # clear sum bit from S
        ror     P, P, 1          # rotate P right 1 bit
        sub     I, I, 1          # decrement shift counter
        bgtz    X, loop          # repeat if X nonzero
        or      P, P, S          # combine partial sum/result
        ror     P, P, I          # final shift
        put     P                # output product
        done

To avoid multiplicative overflow, two 32 bit integers may be multiplied to produce a 64 bit product in two 32 bit words, HI and LO, which hold the most and least significant 32 bits of the product, respectively.

In the HI/LO algorithm, multiplication is performed after splitting the 32 bit numbers to be multiplied into 16 bit HI/LO pairs and performing 32 bit multiplication on the pairs.

An implementation of the HI/LO algorithm in C language is shown below:

The 64 bit HI/LO algorithm may also be implemented in SAL:

The algorithm works without modification for a negative multiplier and a positive multiplicand. It can be extended to work for 2's complement integers. To multiply two negative numbers or a positive multiplier and negative multiplicand, two approaches are possible:

1. Convert negative numbers to positive, multiply positive numbers and then convert result to correct sign.
2. Sign extend both numbers to 64 bits and perform 64 bit multiplication. The correct result will be found in the least significant 64 bits of the product.

An example of method #2 applied to 4-bit 2's complement integers is shown below. The 4-bit integers 1101 (-3) and 0110 (6) are sign extended to 8 bits before multiplication. The correct result (-18) is found in the rightmost 8 bits.

         11111101 (-3)
       x 00000110 (6)
       ----------
         00000000
        11111101
       11111101
      00000000
     00000000
    00000000
   00000000
+ 00000000
-----------------
         11101110 (-18)